题目内容
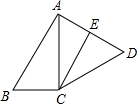如图，四边形ABCD中，AC=CD，AB=2BC，∠BAC与∠B互余，CE∥BA，CE交AD于E，且CD2=CE2+DE2，求证：AD=| 3 |
考点：勾股定理的逆定理,相似三角形的判定与性质
专题：证明题
分析：如图，首先求出∠BAC=30°；进而得到∠ECA=∠BAC=30°；证明△ACD为等边三角形，这是解决本题的关键；
得到AD=AC；证明AC=
BC，问题即可解决．
得到AD=AC；证明AC=
| 3 |
解答：解：如图，
∵∠BAC与∠B互余，
∴∠AB=90°；而AB=2BC，
∴∠BAC=30°；
∵CE∥BA，
∴∠ECA=∠BAC=30°；
∵CD2=CE2+DE2，
∴∠CED=90°；
在直角△ACE与直角△DCE中，
∵
，
∴△ACE≌△DCE（HL），
∴∠DCE=∠ACE=30°，
∴∠ACD=60°，△ACD为等边三角形，
∴AC=AD；在直角△ABC中，
∵AB=2BC，
∴AC2=（2BC）2-BC2=3BC2，
∴AC=
BC，AD=
BC．
解：如图，∵∠BAC与∠B互余，
∴∠AB=90°；而AB=2BC，
∴∠BAC=30°；
∵CE∥BA，
∴∠ECA=∠BAC=30°；
∵CD2=CE2+DE2，
∴∠CED=90°；
在直角△ACE与直角△DCE中，
∵
|
∴△ACE≌△DCE（HL），
∴∠DCE=∠ACE=30°，
∴∠ACD=60°，△ACD为等边三角形，
∴AC=AD；在直角△ABC中，
∵AB=2BC，
∴AC2=（2BC）2-BC2=3BC2，
∴AC=
| 3 |
| 3 |
点评：该题主要考查了勾股定理的逆定理、全等三角形的判定及其性质、直角三角形的性质等几何知识点的应用问题；解题的关键是灵活运用勾股定理的逆定理等知识来分析、解答．
练习册系列答案
相关题目
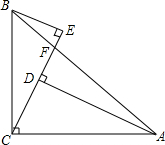如图，∠ACB=90°，AC=BC，F是AB上一点，连接CF，过点A、B分别作AD⊥CF于点D，BE⊥CF于点E．
如图，AB、CD相交于点O，且∠C=∠B，若AC=4cm，AO=3cm，BD=8cm．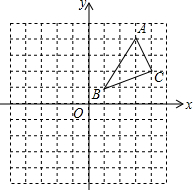
如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（3，4）、B（1，1）、C（4，2）．
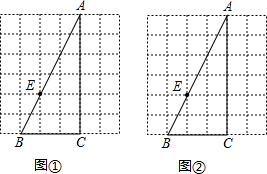如图，已知△ABC中，∠C=90°，点E在边AB上，请过点E作一条直线，与△ABC的其他边相交于一点D，使得以点A、E、D为顶点的三角形与△ABC相似，并求它们的周长之比．
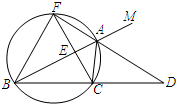如图，已知△ABC的一个外角∠CAM=120°，AD是∠CAM的平分线，且AD的反向延长线与△ABC的外接圆交于点F，连接FB、FC，且FC与AB交于E．