题目内容
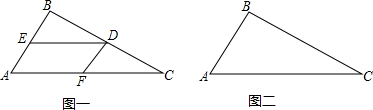
如图，已知，PM=PN，EQ∥MN，MQ为∠PMN的平分线，且∠MQN=72°，则图中的等腰△有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
考点：等腰三角形的判定
专题：
分析：根据等腰三角形的判定定理：在三角形中，如果两个底角相等，那么该三角形是等腰三角形．由此来判断图形中有几个等腰三角形．
解答：解：∵∠P=36°，∠N=72°
∴∠PMN=72°，△PMN为等腰三角形．
∵MQ为∠PMN的平分线，∠P=36°
∴∠PMQ=∠FMN=36°，△PMQ为等腰三角形．
∵EQ∥MN，
∴∠PQE=∠N=72°，∠PEQ=∠PMN=72°
∴△PEQ为等腰三角形．
∵EQ∥MN，∠QMN=36°，∠N=72°
∴∠EQM=∠QMN=36°，∠MQN=72°
∴△MQN为等腰三角形．
∵∠PMQ=∠QMN=36°，∠EQM=∠QMN=36°
∴∠EMQ=∠EQM
∴△EMQ为等腰三角形．
综上得出图形中的等腰三角形为：△PMN，△EMQ，△MQN，△QPM，△PEQ．
故选D．
∴∠PMN=72°，△PMN为等腰三角形．
∵MQ为∠PMN的平分线，∠P=36°
∴∠PMQ=∠FMN=36°，△PMQ为等腰三角形．
∵EQ∥MN，
∴∠PQE=∠N=72°，∠PEQ=∠PMN=72°
∴△PEQ为等腰三角形．
∵EQ∥MN，∠QMN=36°，∠N=72°
∴∠EQM=∠QMN=36°，∠MQN=72°
∴△MQN为等腰三角形．
∵∠PMQ=∠QMN=36°，∠EQM=∠QMN=36°
∴∠EMQ=∠EQM
∴△EMQ为等腰三角形．
综上得出图形中的等腰三角形为：△PMN，△EMQ，△MQN，△QPM，△PEQ．
故选D．
点评：本题考查了三角形的内角和为180°，平行线的性质定理，等腰三角形的判定定理；求得各角的度数是正确解答本题的关键．
练习册系列答案
相关题目
如图，AB、CD相交于点O，且∠C=∠B，若AC=4cm，AO=3cm，BD=8cm．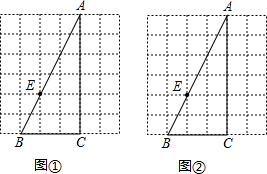
如图，已知△ABC中，∠C=90°，点E在边AB上，请过点E作一条直线，与△ABC的其他边相交于一点D，使得以点A、E、D为顶点的三角形与△ABC相似，并求它们的周长之比．
如图所示，一座抛物线型拱桥，拱顶O离水面高4米，水面宽度AB=10米，现有一竹排运送一只货箱欲从桥下经过，已知货箱长10米，宽6米，高2.4米（竹排与水面持平），问货箱能否顺利通过该桥？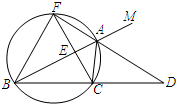
如图，已知△ABC的一个外角∠CAM=120°，AD是∠CAM的平分线，且AD的反向延长线与△ABC的外接圆交于点F，连接FB、FC，且FC与AB交于E．
如图，直线AB、CD、EF相交于O点，已知∠AOE=20°，∠DOB=52°，OG平分∠COF．求∠EOG的度数．
在⊙O中，弦AB=2cm，∠ACB=30°，则⊙O的直径为