题目内容
某超市出售一批进价为4元/盒的牙膏,在市场营销中发现此商品的销售单价x(元)与目前销售量y(盒)之间有如下反比例函数关系:
(1)试确定y与x之间的函数解析式;
(2)设这批牙膏的日销售利润为w元,试求出w与x之间的函数解析式,并探究此函数的增减性;
(3)若物价局规定此牙膏的售价最高不能超过7元/盒,请根据(2)中探究出的结论,确定当日的销售单位为多少时,日销售利润最大.
| x(元) | 4.5 | 5 | 6 | 6.3 |
| y(盒) | 280 | 252 | 210 | 200 |
(2)设这批牙膏的日销售利润为w元,试求出w与x之间的函数解析式,并探究此函数的增减性;
(3)若物价局规定此牙膏的售价最高不能超过7元/盒,请根据(2)中探究出的结论,确定当日的销售单位为多少时,日销售利润最大.
考点:反比例函数的应用
专题:
分析:(1)根据表可以得到x与对应的y的值的乘积是常数,据此即可求得函数的解析式;
(2)根据利润=每盒的利润×销售的盒数,即可求得函数解析式,根据反比例函数的性质确定增减性;
(3)根据(2)的结果即可确定x的值,进而求解.
(2)根据利润=每盒的利润×销售的盒数,即可求得函数解析式,根据反比例函数的性质确定增减性;
(3)根据(2)的结果即可确定x的值,进而求解.
解答:解:(1)设y=
(k为常数且k≠0),把点(4.5,280)代入得,k=1260,
所以y与x的函数关系式是y=
;
(2)∵W=(x-4)y=
,
即w=1260-
,
因为z=
(x>0),中z随x的增大而减小,则w随x的增大而增大;
(3)又∵x≤7,
∴当x=7时,w最大,则w=1260-
=560(元).
| k |
| x |
所以y与x的函数关系式是y=
| 1260 |
| x |
(2)∵W=(x-4)y=
| 1260(x-4) |
| x |
即w=1260-
| 5040 |
| x |
因为z=
| 5040 |
| x |
(3)又∵x≤7,
∴当x=7时,w最大,则w=1260-
| 5040 |
| 7 |
点评:本题是反比例函数的实际应用,理解利润的计算方法,确定w与x的函数的则增减性是关键.

练习册系列答案
相关题目
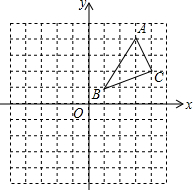 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,4)、B(1,1)、C(4,2).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,4)、B(1,1)、C(4,2).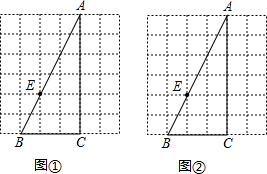 如图,已知△ABC中,∠C=90°,点E在边AB上,请过点E作一条直线,与△ABC的其他边相交于一点D,使得以点A、E、D为顶点的三角形与△ABC相似,并求它们的周长之比.
如图,已知△ABC中,∠C=90°,点E在边AB上,请过点E作一条直线,与△ABC的其他边相交于一点D,使得以点A、E、D为顶点的三角形与△ABC相似,并求它们的周长之比. 作出函数y=
作出函数y=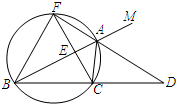 如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.
如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.