题目内容
已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向上;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<2,y随x的增大而减小;⑤当x=0时,y最小值为1.则其中说法正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数的性质
专题:计算题
分析:利用抛物线的顶点式和二次函数的性质分别进行判断.
解答:解:∵a=2>,
∴抛物线开口向上,所以①正确;
∵y=2(x-3)2+1,
∴抛物线的对称轴为直线x=3,顶点坐标为(3,1),所以②③错误;
当x<3时,y随x的增大而减小,所以④错误;
当x=3时,y有最小值1,所以⑤错误.
故选A.
∴抛物线开口向上,所以①正确;
∵y=2(x-3)2+1,
∴抛物线的对称轴为直线x=3,顶点坐标为(3,1),所以②③错误;
当x<3时,y随x的增大而减小,所以④错误;
当x=3时,y有最小值1,所以⑤错误.
故选A.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
有一密码箱的密码有5位数字,若忘记了其中第一位和最后一位,那么一次把它打开的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确都是( )
| A、大于90°的角是钝角 |
| B、任何一个角都可以用一个大写字母表示 |
| C、平角是两条边互为反向延长线的角 |
| D、有公共顶点的两个直角组成平角 |
 如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为
如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为 如图,平面内有4个点A、B、C、D,按下列语句在指定位置上画出图形.
如图,平面内有4个点A、B、C、D,按下列语句在指定位置上画出图形.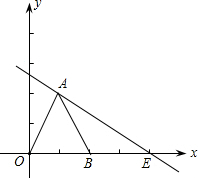 如图,△OAB是边长为2的等边三角形,过点A的直线y=-
如图,△OAB是边长为2的等边三角形,过点A的直线y=-