题目内容
(1)操作发现:如图1,D是等边三角形ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边三角形DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图2,当动点D运动到等边三角形ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,是否有新的结论?如果有新的结论,直接写出新的结论,不需证明.
(3)深入探究:
①如图3,当动点D在等边三角形ABC的边BA上运动时(点D与点B不重合),连接DC,以DC为边在其上方、下方分别作等边三角形DCF和等边三角形DCF',连接AF,BF′.探究AF,BF′与AB有何数量关系?直接写出你的结论,不需证明.
②如图4,当动点D在等边三角形ABC的边BA的延长线上运动时,其他作法与图3相同,①中的结论是否仍然成立?如果成立,请证明;如果不成立,是否有新的结论?如果有新的结论,直接写出新的结论,不需证明.

(2)类比猜想:如图2,当动点D运动到等边三角形ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,是否有新的结论?如果有新的结论,直接写出新的结论,不需证明.
(3)深入探究:
①如图3,当动点D在等边三角形ABC的边BA上运动时(点D与点B不重合),连接DC,以DC为边在其上方、下方分别作等边三角形DCF和等边三角形DCF',连接AF,BF′.探究AF,BF′与AB有何数量关系?直接写出你的结论,不需证明.
②如图4,当动点D在等边三角形ABC的边BA的延长线上运动时,其他作法与图3相同,①中的结论是否仍然成立?如果成立,请证明;如果不成立,是否有新的结论?如果有新的结论,直接写出新的结论,不需证明.

考点:全等三角形的判定与性质
专题:几何综合题
分析:(1)证明△BCD≌△ACF即可解题;
(2)证明△BCD≌△ACF即可解题;
(3)①证明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可解题;
②证明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可证明新结论.
(2)证明△BCD≌△ACF即可解题;
(3)①证明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可解题;
②证明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可证明新结论.
解答:解:(1)∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
,
∴△BCD≌△ACF,(SAS),
∴BD=AF;
(2)∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
,
∴△BCD≌△ACF(SAS),
∴BD=AF;
(3)①∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
,
∴△BCD≌△ACF(SAS),
∴BD=AF
∵∠BCA=∠DCF',
∴∠BCF'=∠ACD,
在△BCF'和△ACD中,
,
∴△BCF'≌△ACD(SAS),
∴AD=BF',
∴AB=AF+BF';
②不成立,新结论为AB=AF-BF'.
证明∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
,
∴△BCD≌△ACF(SAS),
∴BD=AF;
∵∠BCA=∠DCF',
∴∠BCF'=∠ACD,
在△BCF'和△ACD中,
,
∴△BCF'≌△ACD(SAS),
∴AD=BF',
∴AB=AF-BF'.
∴∠BCD=∠ACF,
在△BCD和△ACF中,
|
∴△BCD≌△ACF,(SAS),
∴BD=AF;
(2)∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
|
∴△BCD≌△ACF(SAS),
∴BD=AF;
(3)①∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
|
∴△BCD≌△ACF(SAS),
∴BD=AF
∵∠BCA=∠DCF',
∴∠BCF'=∠ACD,
在△BCF'和△ACD中,
|
∴△BCF'≌△ACD(SAS),
∴AD=BF',
∴AB=AF+BF';
②不成立,新结论为AB=AF-BF'.
证明∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
|
∴△BCD≌△ACF(SAS),
∴BD=AF;
∵∠BCA=∠DCF',
∴∠BCF'=∠ACD,
在△BCF'和△ACD中,
|
∴△BCF'≌△ACD(SAS),
∴AD=BF',
∴AB=AF-BF'.
点评:本题考查了全等三角形判定,考查了全等三角形对应边相等的性质,本题中每一问都找出全等三角形并求证是解题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
下列说法正确都是( )
| A、大于90°的角是钝角 |
| B、任何一个角都可以用一个大写字母表示 |
| C、平角是两条边互为反向延长线的角 |
| D、有公共顶点的两个直角组成平角 |
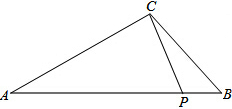 如图,在△ABC中,∠A=30°,∠B=45°,AC=8,点P在线段AB上,连接CP,且tan∠APC=
如图,在△ABC中,∠A=30°,∠B=45°,AC=8,点P在线段AB上,连接CP,且tan∠APC=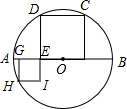 如图,已知AB是⊙O的直径,AB=8,点C、H是⊙O上的动点,四边形CDEF和EGHI都是正方形,其中点G、E、F在AB上,则正方形CDEF和正方形EGHI面积和为
如图,已知AB是⊙O的直径,AB=8,点C、H是⊙O上的动点,四边形CDEF和EGHI都是正方形,其中点G、E、F在AB上,则正方形CDEF和正方形EGHI面积和为 如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为
如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为