题目内容
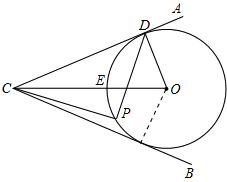 如图:∠ACB=60°,CE平分∠ACB,O为射线CE上的一点,⊙O切AC于点D
如图:∠ACB=60°,CE平分∠ACB,O为射线CE上的一点,⊙O切AC于点D(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,P为⊙O上一点,且使得∠DPC=90°,求DP的长.
考点:切线的判定
专题:
分析:(1)过O作OM⊥BC,交BC于点M,由条件证明△DCO≌△MCO,可得OM=OD,可得BC为切线;
(2)在△COD中,可求得CD,取CD的中点为N,连接PN,ON,交DP于点Q,结合条件可证得NP为切线,则可知Q为DP中点,在Rt△NOD中可求得NO,再利用面积相等可求得DQ,从而可求得DP.
(2)在△COD中,可求得CD,取CD的中点为N,连接PN,ON,交DP于点Q,结合条件可证得NP为切线,则可知Q为DP中点,在Rt△NOD中可求得NO,再利用面积相等可求得DQ,从而可求得DP.
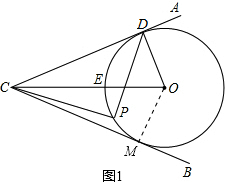
解答:(1)证明:如图1,过O作OM⊥BC交点M,
在△DCO和△MCO中,
,
∴△DCO≌△MCO(AAS),
∴OM=OD,且CD为切线,
∴OD等于圆的半径,
∴O点到BC的距离等于半径,
∴BC是⊙O的切线;
(2)解:如图2,取CD的中点为N,连接PN,ON,交DP于点Q,

∵∠DPC=90°,
∴PN=ND,且OD=OP,
∴NO垂直平分DP,
在Rt△COD中,OD=6,∠DCO=60°,
∴CD=6
,则ND=3
,
在Rt△ODN中,由勾股定理可求得ON=3
,
由面积相等可得ND•OD=NO•DQ,
即3
×6=3
•DQ,
解得DQ=
,
∴DP=2DQ=
.

在△DCO和△MCO中,
|
∴△DCO≌△MCO(AAS),
∴OM=OD,且CD为切线,
∴OD等于圆的半径,
∴O点到BC的距离等于半径,
∴BC是⊙O的切线;
(2)解:如图2,取CD的中点为N,连接PN,ON,交DP于点Q,

∵∠DPC=90°,
∴PN=ND,且OD=OP,
∴NO垂直平分DP,
在Rt△COD中,OD=6,∠DCO=60°,
∴CD=6
| 3 |
| 3 |
在Rt△ODN中,由勾股定理可求得ON=3
| 7 |
由面积相等可得ND•OD=NO•DQ,
即3
| 3 |
| 7 |
解得DQ=
6
| ||
| 7 |
∴DP=2DQ=
12
| ||
| 7 |
点评:本题主要考查切线的判定和性质,掌握作出距离证明距离等于半径也是证明切线的方法是解题的关键,在第(2)中取CD的中点,得到NO是DP的垂直平分线是解题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
据第六次全国人口普查公布的数据,广东省常住人口约为104300000人,位居全国之首,将104300000用科学记数法表示为( )
| A、0.1043×109 |
| B、10.43×107 |
| C、1.043×109 |
| D、1.043×108 |
有一密码箱的密码有5位数字,若忘记了其中第一位和最后一位,那么一次把它打开的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

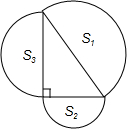 如图所示,分别以直角三角形三边为直径作半圆,三个半圆的面积分别为S1、S2、S3.已知S1=25,S2=9,则S3=
如图所示,分别以直角三角形三边为直径作半圆,三个半圆的面积分别为S1、S2、S3.已知S1=25,S2=9,则S3= 如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为
如图:在正三角形ABC中,AB=BC=AC=4,则点A的坐标为