题目内容
8.体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“+“表示成绩大于15秒.| -0.8 | +1 | -1.2 | -0.1 | -0.6 | +0.6 | -0.3 | -0.2 |
(2)这个小组男生的达标率为多少?(达标率=$\frac{达标人数}{总人数}$)
(3)这个小组男生的平均成绩是多少秒?
分析 (1)先比较大小,进一步得到这个小组男生最优秀的成绩是多少秒,最差的成绩是多少秒;
(2)根据非正数是达标成绩,可得达标人数,根据达标人数除以总人数,可得达标率;
(3)根据有理数的加法,可得总成绩,根据总成绩除以人数,可得平均分.
解答 解:(1)15-0.8=14.2(秒),
15+0.6=15.6(秒).
答:这个小组男生最优秀的成绩是14.2秒,最差的成绩是15.6秒;
(2)-0.8,+1,-1.2,-0.1,-0.6,+0.6,-0.3,-0.2,得达标人数是6.
达标率是:6÷18×100%=75%.
答:这个小组男生的达标率为75%;
(2)平均成绩为:
15+(-0.8+1-1.2-0.1-0.6+0.6-0.3-0.2)÷8
=15-0.2
=14.8(秒).
答:这个小组男生的平均成绩是14.8秒.
点评 本题考查了正数和负数,关键是利用达标率、平均数的公式求解.达标率为达标人数除以总人数.注意小于等于15秒的为达标.平均数表示一组数据的平均程度.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
13.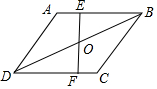 如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )
如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )
 如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )
如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )| A. | 12+$\frac{3}{2}$$\sqrt{3}$ | B. | 12+3$\sqrt{3}$ | C. | 15 | D. | 18 |

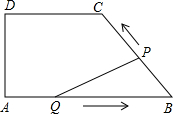 如图,在四边形ABCD中,DC∥AB,AD=4,DC=5,AB=8.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为每秒1个单位长度.当P点到达C点时,两点同时停止运动,连接PQ.设运动时间为t秒,当△PQB为等腰三角形时,t的值为$\frac{40}{11}$、$\frac{48}{11}$或4.
如图,在四边形ABCD中,DC∥AB,AD=4,DC=5,AB=8.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为每秒1个单位长度.当P点到达C点时,两点同时停止运动,连接PQ.设运动时间为t秒,当△PQB为等腰三角形时,t的值为$\frac{40}{11}$、$\frac{48}{11}$或4.
 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:BE=CE (要求:不用三角形全等的方法)
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:BE=CE (要求:不用三角形全等的方法)