题目内容
13.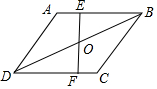 如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )
如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )| A. | 12+$\frac{3}{2}$$\sqrt{3}$ | B. | 12+3$\sqrt{3}$ | C. | 15 | D. | 18 |
分析 直接利用菱形的性质结合直角三角形的性质得出AN的长,再利用全等三角形的判定与性质得出BE=DF,进而得出答案.
解答  解:过点A作AN⊥DC于点N,
解:过点A作AN⊥DC于点N,
∵四边形ABCD是菱形,
∴AD=DC=BC=AB=6,
∵∠C=120°,
∴∠ADC=60°,
∴DN=3,
则AN=3$\sqrt{3}$,
∵FE⊥AB,
故可得EF=3$\sqrt{3}$,
∵四边形ABCD是菱形,
∴AB∥DC,
∴∠EBO=∠CDO,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠EBO=∠ODC}\\{BO=DO}\\{∠EOB=∠DOF}\end{array}\right.$,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∴四边形AEFD的周长为:AE+EF+DF+AD=AD+AB+EF=12+3$\sqrt{3}$.
故选:B.
点评 此题主要考查了菱形的性质以及全等三角形的判定与性质,正确得出△BOE≌△DOF是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
11. 下面圆柱体的侧面积为( )
下面圆柱体的侧面积为( )
 下面圆柱体的侧面积为( )
下面圆柱体的侧面积为( )| A. | 31.4 | B. | 62.8 | C. | 39.25 | D. | 15.7 |
4.在科技迅猛发展的今天,移动电话成为了人们生活中非常普及的通讯工具,选择经济实惠的计费方式成为了人们所关心的具有实际意义的问题.下表是两种移动电话的计费方式:
若小明的爸爸每月打电话的时间在300分钟,请问选择哪种方式省钱( )
| 月使用费(元) | 主叫限定时间(分钟) | 主叫超时费/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
| A. | 方式一 | B. | 方式二 | C. | 两种方式一样 | D. | 无法确定 |
8.体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“+“表示成绩大于15秒.
问:(1)这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
(2)这个小组男生的达标率为多少?(达标率=$\frac{达标人数}{总人数}$)
(3)这个小组男生的平均成绩是多少秒?
| -0.8 | +1 | -1.2 | -0.1 | -0.6 | +0.6 | -0.3 | -0.2 |
(2)这个小组男生的达标率为多少?(达标率=$\frac{达标人数}{总人数}$)
(3)这个小组男生的平均成绩是多少秒?
18.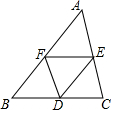 如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
 如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )| A. | △BDF | B. | △DEF | C. | △CDE | D. | △BDF和△CDE |
 如图,∠AOB内一点P:过点P画PC∥OB交OA于点C,画PD⊥OA,垂足为D.
如图,∠AOB内一点P:过点P画PC∥OB交OA于点C,画PD⊥OA,垂足为D.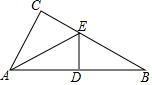 如图:已知,∠C=90°,AD=AC,DE⊥AB交BC于点E.若∠B=40°,则∠EAC=25°.
如图:已知,∠C=90°,AD=AC,DE⊥AB交BC于点E.若∠B=40°,则∠EAC=25°. 如图,在等腰△ABC中,AB=AC,点D,E分别是BC,AB边的中点,过A点作AF∥BC交DE的延长线于F点,连接AD,BF.
如图,在等腰△ABC中,AB=AC,点D,E分别是BC,AB边的中点,过A点作AF∥BC交DE的延长线于F点,连接AD,BF.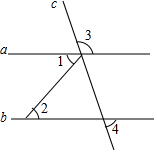 如图,若∠1=40°30′,∠2=40°30′,∠3=120°,则∠4=60°.
如图,若∠1=40°30′,∠2=40°30′,∠3=120°,则∠4=60°.