题目内容
11.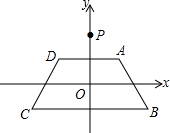 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )| A. | (2014,2) | B. | (2014,-2) | C. | (2012,-2) | D. | (2012,2) |
分析 由P、A两点坐标可知,点P绕点A旋转180°得点P1,即为点P关于A的对称点,依此类推,点P2为P1关于B的对称点,由此发现一般规律.
解答 解:由已知可以得到,点P1,P2的坐标分别为(2,0),(2,-2).
记P2(a2,b2),其中a2=2,b2=-2.
根据对称关系,依次可以求得:P3(-4-a2,-2-b2),P4(2+a2,4+b2),P5(-a2,-2-b2),P6(4+a2,b2).
令P6(a6,b2),同样可以求得,点P10的坐标为(4+a6,b2),即P10(4×2+a2,b2),
所以点P2010的坐标是(2010,-2),
所以P2014(2012+2,-2),即P2014(2014,-2),
故选B.
点评 本题考查了旋转变换的规律.关键是根据等腰梯形,点的坐标的特殊性,寻找一般规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
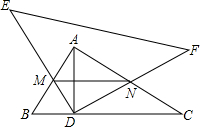 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC上的高,另有一Rt△DEF(其直角顶点在D点)绕D点旋转,在旋转过程中,DE,DF分别与边AB,AC交于M、N点,则线段MN的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC上的高,另有一Rt△DEF(其直角顶点在D点)绕D点旋转,在旋转过程中,DE,DF分别与边AB,AC交于M、N点,则线段MN的最小值为$\frac{24}{5}$.
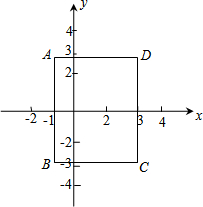 在平面直角坐标系中,长方形ABCD的边BC∥x轴,若A点的坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$).
在平面直角坐标系中,长方形ABCD的边BC∥x轴,若A点的坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$).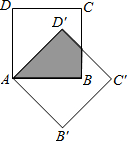 如图,边长为2的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是4$\sqrt{2}$-4.
如图,边长为2的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是4$\sqrt{2}$-4.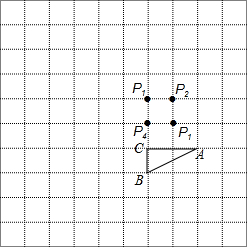 如图,在10×10的小正方形网格中,△ABC的顶点A、B、C在网格点上,P1、P2、P3、P4是其中一个小正方形的四个格点,将△ABC绕A点逆时针旋转90°,再向下平移2个单位,得到△A′B′C′;将△ABC按一定的规律顺次旋转,第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1;第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2;第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3,依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去.
如图,在10×10的小正方形网格中,△ABC的顶点A、B、C在网格点上,P1、P2、P3、P4是其中一个小正方形的四个格点,将△ABC绕A点逆时针旋转90°,再向下平移2个单位,得到△A′B′C′;将△ABC按一定的规律顺次旋转,第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1;第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2;第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3,依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去.
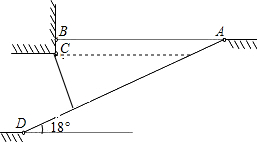 为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)
为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)