题目内容
11．
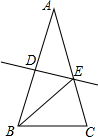如图，在△ABC中，AB=AC，DE垂直平分AB，分别交AB、AC于点D、E，若∠EBC=30°，则∠A=（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |
分析 设∠A为x，根据线段的垂直平分线的性质得到EA=EB，用x表示出∠BEC，根据等腰三角形的性质得到∠ABC=∠C，根据三角形内角和定理列出方程，解方程即可．
解答 解：设∠A为x，
∵DE垂直平分AB，
∴EA=EB，
∴∠EBA=∠A=x，
∴∠BEC=2x，
∵AB=AC，
∴∠ABC=∠C，
∴30°+x+30°+2x=180°，
解得，x=40°，
故选：C．
点评 此题主要考查线段的垂直平分线的性质和三角形内角和定理的应用，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
相关题目
2．在平面直角坐标系中，点P（-2，5）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
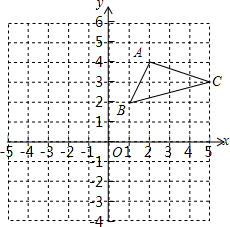如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4）．
如图，已知点P在AB上，∠APD=∠APC，∠DBA=∠CBA，求证：AC=AD．
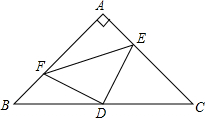已知：如图，Rt△ABC中，∠BAC=90°，AB=AC，D是BC的中点，AE=BF．
如图，已知∠EFD=∠BCA，BC=EF，AF=DC，则AB=DE．请通过完成以下填空的形式说明理由．