题目内容
3.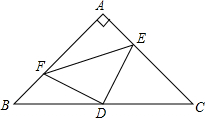 已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.
已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.(1)求证:DE=DF;
(2)若BC=8,求四边形AFDE的面积.
分析 (1)连接AD,证明△BFD≌△AED,根据全等三角形的性质即可得出DE=DF;
(2)根据△DAE≌△DBF,得到四边形AFDE的面积=S△ABD=$\frac{1}{2}$S△ABC,于是得到结论.
解答 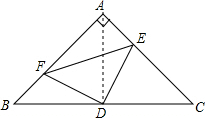 证明:(1)连接AD,
证明:(1)连接AD,
∵Rt△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵AB=AC,DB=CD,
∴∠DAE=∠BAD=45°,
∴∠BAD=∠B=45°,
∴AD=BD,∠ADB=90°,
在△DAE和△DBF中,
$\left\{\begin{array}{l}{AE=BF}\\{∠DAE=∠B=45°}\\{AD=BD}\end{array}\right.$,
∴△DAE≌△DBF(SAS),
∴DE=DF;
(2)∵△DAE≌△DBF,
∴四边形AFDE的面积=S△ABD=$\frac{1}{2}$S△ABC,
∵BC=8,
∴AD=$\frac{1}{2}$BC=4,
∴四边形AFDE的面积=S△ABD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×\frac{1}{2}×8×4$=8.
点评 本题主要考查了全等三角形的判定和等腰三角形的判定.考查了学生综合运用数学知识的能力,连接AD,构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
8. 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
11.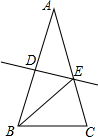 如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
 如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
18. 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )
 如图是一个“中”的几何体,则该几何体的俯视图为( )
如图是一个“中”的几何体,则该几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
8.下列各式正确的是( )
| A. | |5|=|-5| | B. | -|5|=|-5| | C. | -5=|-5| | D. | 5=-|-5| |
 将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.
将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.