题目内容
16. 如图,已知点P在AB上,∠APD=∠APC,∠DBA=∠CBA,求证:AC=AD.
如图,已知点P在AB上,∠APD=∠APC,∠DBA=∠CBA,求证:AC=AD.
分析 由平角的定义得到∠BPD=∠BPC,推出△BDP≌△BCP,根据全等三角形的性质得到BD=BC,证得△ADB≌△ACB,根据全等三角形的性质得到结论.
解答 证明:∵∠APD=∠APC,
∴∠BPD=∠BPC,
在△BDP与△BCP中,$\left\{\begin{array}{l}{∠BPD=∠BPC}\\{PB=PB}\\{∠DBA=∠CBA}\end{array}\right.$,
∴△BDP≌△BCP,
∴BD=BC,
在△ADB与△ACB中,$\left\{\begin{array}{l}{BD=BC}\\{∠ABD=∠ABC}\\{AB=AB}\end{array}\right.$,
∴△ADB≌△ACB,
∴AC=AD.
点评 本题考查了全等三角形的判定和性质,平角的定义,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
1.两个相似多边形的周长比是2:3,其中较小多边形的面积为4cm2,则较大多边形的面积为( )
| A. | 9cm2 | B. | 16cm2 | C. | 56cm2 | D. | 24cm2 |
7.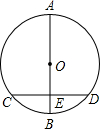 如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
 如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
如图,AB为⊙0的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )| A. | 6 | B. | 8 | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{5}$ |
4.下列说法中,正确的是( )
| A. | 两条射线组成的图形叫做角 | B. | 两点确定一条直线 | ||
| C. | 两点之间直线最短 | D. | 延长直线AB至C |
11.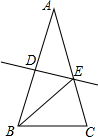 如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
 如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )
如图,在△ABC中,AB=AC,DE垂直平分AB,分别交AB、AC于点D、E,若∠EBC=30°,则∠A=( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
8.下列各式正确的是( )
| A. | |5|=|-5| | B. | -|5|=|-5| | C. | -5=|-5| | D. | 5=-|-5| |
6.下列关于x的一元二次方程中,有两个不相等的实数根的是( )
| A. | x2+3=0 | B. | x2-4x+4=0 | C. | x2-2014=0 | D. | x2+2x+3=0 |
 如图,已知点A在反比例函数y=$\frac{10}{x}$(x<0)的图象上,AD∥x轴,AB∥y轴,点B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,过点B作BC∥x轴,交y轴于点C,若四边形ABCD的面积为8,则k的值为18.
如图,已知点A在反比例函数y=$\frac{10}{x}$(x<0)的图象上,AD∥x轴,AB∥y轴,点B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,过点B作BC∥x轴,交y轴于点C,若四边形ABCD的面积为8,则k的值为18.