题目内容
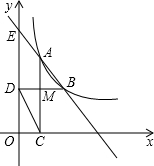 已知:如图,在平面直角坐标系中,直线AB与反比例函数y=
已知:如图,在平面直角坐标系中,直线AB与反比例函数y=| m |
| x |
(1)求该反比例函数的解析式;
(2)求证:CD∥AB.
考点:反比例函数综合题
专题:
分析:(1)利用待定系数法即可求得函数的解析式;
(2)利用a表示出B、D、M的坐标,证明△CDM∽△ABM,然后利用平行线的判定定理证明.
(2)利用a表示出B、D、M的坐标,证明△CDM∽△ABM,然后利用平行线的判定定理证明.
解答:解:(1)把(1,4)代入反比例函数解析式,得:m=4,
则反比例函数的解析式是:y=
;
(2)根据题意得:B(a,
),C(1,0),D(0,
),M(1,
).
则DM=1,BM=a-1,AM=4-
,CM=
.
∵
=
,
=
,
∴
=
,
又∵∠DMC=∠BMA,
∴△CDM∽△ABM,
∴∠CDM=∠ABM,
∴CD∥AB.
则反比例函数的解析式是:y=
| 4 |
| x |
(2)根据题意得:B(a,
| 4 |
| a |
| 4 |
| a |
| 4 |
| a |
则DM=1,BM=a-1,AM=4-
| 4 |
| a |
| 4 |
| a |
∵
| DM |
| BM |
| 1 |
| a-1 |
| CM |
| AM |
| 1 |
| a-1 |
∴
| DM |
| BM |
| CM |
| AM |
又∵∠DMC=∠BMA,
∴△CDM∽△ABM,
∴∠CDM=∠ABM,
∴CD∥AB.
点评:本题是反比例函数与相似三角形的判定与性质的综合应用,正确证明两个三角形相似是本题的关键.

练习册系列答案
相关题目
如图所示,其中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在等腰直角△ABC中,∠C=90°,O是斜边AB的中点,将直角三角板的直角顶点与点O重合,两直角边分别与边AC、BC交于点E、F,试判断AE与CF的数量关系,并进行证明.
如图,在等腰直角△ABC中,∠C=90°,O是斜边AB的中点,将直角三角板的直角顶点与点O重合,两直角边分别与边AC、BC交于点E、F,试判断AE与CF的数量关系,并进行证明.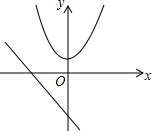 如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.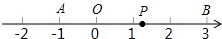 如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
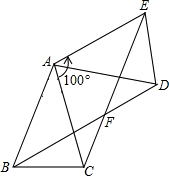 如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.