题目内容
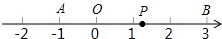 如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.(1)请根据题意填空:线段OA的长度是
(2)当点P以每分钟2个单位长度的速度从原点O向左运动的同时,点A以每分钟3个单位长度的速度向左运动,点B以每分钟2个单位长度的速度向左运动,求多少分钟时点P到点A和点B的距离相等,如果设t分钟时点P到点A和点B的距离相等;
①请你用含t的式子表示:
此时,在数轴上点A对应的数是
②请你求出t的值.
考点:一元一次方程的应用,数轴
专题:
分析:(1)由数轴上任意两点间的距离=这两点表示的数的差的绝对值就可以求出结论;
(2)①由在数轴上表示的数向左运动减,向右运动加的法则就可以分别表示出A、B、P对应的数,由数轴上两点间的距离公式就可以得出PA、PB;
②由①的PA=PB建立方程求出其解即可.
(2)①由在数轴上表示的数向左运动减,向右运动加的法则就可以分别表示出A、B、P对应的数,由数轴上两点间的距离公式就可以得出PA、PB;
②由①的PA=PB建立方程求出其解即可.
解答:解:(1)由题意,得
OA=0-(-1)=1,OB=3-0=3,AB=3-(-1)=4,
x-(-1)=3-x
解得:x=1.
故答案为:1,3,4,1;
(2)①由题意,得
点A对应的数是-1-3t,点B对应的数是3-2t,点P对应的数是-2t,线段PA=t+1,线段PB=3.
故答案为:-1-3t,3-2t,-2t,t+1,3;
②由题意,得
t+1=3,
解得t=2.
答:t的值为2.
OA=0-(-1)=1,OB=3-0=3,AB=3-(-1)=4,
x-(-1)=3-x
解得:x=1.
故答案为:1,3,4,1;
(2)①由题意,得
点A对应的数是-1-3t,点B对应的数是3-2t,点P对应的数是-2t,线段PA=t+1,线段PB=3.
故答案为:-1-3t,3-2t,-2t,t+1,3;
②由题意,得
t+1=3,
解得t=2.
答:t的值为2.
点评:本题考查了数轴的运用,数轴上任意两点间距离公式的运用,列一元一次方程解实际问题的运用,解答时运用数轴上两点间的距离相等建立方程是关键.

练习册系列答案
相关题目
 如图,已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD=3∠DOE,求∠AOF的度数.
如图,已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD=3∠DOE,求∠AOF的度数. 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线x=-2.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线x=-2.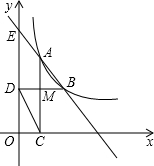 已知:如图,在平面直角坐标系中,直线AB与反比例函数y=
已知:如图,在平面直角坐标系中,直线AB与反比例函数y=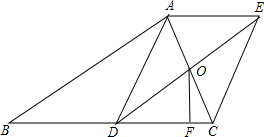 在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE.
在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE. 如图,点C是线段AB的中点,点E是线段CD上一点,连接AE,若DE=2EC,△BCD的面积为2,则△ACE的面积为
如图,点C是线段AB的中点,点E是线段CD上一点,连接AE,若DE=2EC,△BCD的面积为2,则△ACE的面积为 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=4,则点P到AB的距离是
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=4,则点P到AB的距离是