题目内容
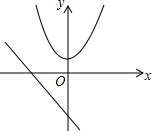 如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.(1)求m取何值时,抛物线c与直线l没有公共点;
(2)变化m,当抛物线c的顶点在直线l上时,求直线l被它截得的线段长.
考点:二次函数的性质
专题:
分析:(1)把两函数的交点问题转化为一元二次方程根的情况:有两解析式组成方程组,消去y得到x2+m=-2x-2,整理得x2+2x+m+2=0,然后根据判别式的意义得△=22-4(m+2)<0,最后解关于m的不等式即可.
(2)根据题意求得抛物线的顶点坐标为(0,-2),代入抛物线的解析式即可求得m,联立方程,解方程即可求得交点坐标,然后根据勾股定理即可求得.
(2)根据题意求得抛物线的顶点坐标为(0,-2),代入抛物线的解析式即可求得m,联立方程,解方程即可求得交点坐标,然后根据勾股定理即可求得.
解答:解:(1)根据题意得x2+m=-2x-2,
整理得x2+2x+m+2=0,
因为抛物线c与直线l没有公共点,
所以△=22-4(m+2)<0,
解得m>-1.
所以当m>-1时,抛物线c与直线l没有公共点;
(2)∵抛物线c的顶点在直线l上,
∴抛物线c的顶点为(0,-2),
代入解析式得,m=-2,
∴抛物线的解析式为y=x2-2,
解
得
或
,
∴直线l和抛物线的交点为(0,-2)和(-2,2),
∴直线l被抛物线截得的线段长=
=2
.
整理得x2+2x+m+2=0,
因为抛物线c与直线l没有公共点,
所以△=22-4(m+2)<0,
解得m>-1.
所以当m>-1时,抛物线c与直线l没有公共点;
(2)∵抛物线c的顶点在直线l上,
∴抛物线c的顶点为(0,-2),
代入解析式得,m=-2,
∴抛物线的解析式为y=x2-2,
解
|
|
|
∴直线l和抛物线的交点为(0,-2)和(-2,2),
∴直线l被抛物线截得的线段长=
| (-2-0)2+(2+2)2 |
| 5 |
点评:本题考查了二次函数的性质,把两函数的交点问题转化为一元二次方程根的情况是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①a-c<0;②c-ab<0;③a-b+c>0;④a+b+c>0,其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①a-c<0;②c-ab<0;③a-b+c>0;④a+b+c>0,其中所有正确结论的序号是( )| A、②④ | B、②③④ |
| C、①②④ | D、①④ |
计算
=( )
| 2011×2012×2013×2014+1 |
| A、4050155 |
| B、4050145 |
| C、4050125 |
| D、4050115 |
 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分几何图形的周长为( )A、
| ||||
B、4-
| ||||
C、1-
| ||||
| D、4 |
 已知:如图,在平面直角坐标系中,直线AB与反比例函数y=
已知:如图,在平面直角坐标系中,直线AB与反比例函数y= 如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7). 如图,在Rt△ABC中,∠ACB=90°,AB=10,cosB=
如图,在Rt△ABC中,∠ACB=90°,AB=10,cosB=