题目内容
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出的特征数为[m-1,1+m,-2m]的函数的一些结论:
①当m=3时,函数图象的顶点坐标是(-1,-8);
②无论m取何值,函数图象与x轴始终有交点;
③当m>1时,函数图象截x轴所得的线段长度大于3;
④函数图象一定经过两个定点.
其中正确的结论有 .
①当m=3时,函数图象的顶点坐标是(-1,-8);
②无论m取何值,函数图象与x轴始终有交点;
③当m>1时,函数图象截x轴所得的线段长度大于3;
④函数图象一定经过两个定点.
其中正确的结论有
考点:二次函数的性质
专题:新定义
分析:①把m=3代入[m-1,1+m,-2m],求得[a,b,c],求得解析式,利用顶点坐标公式解答即可;
②令函数值为0,求得(m-1)x2+(1+m)x-2m=0,根据△≥0,即可解答.
③令函数值为0,求得(m-1)x2+(1+m)x-2m=0,解得x1=-1,x2=
,求得与x轴交点坐标,利用两点间距离公式解决问题;
④根据特征数的特点,直接得出x的值,进一步验证即可解答.
②令函数值为0,求得(m-1)x2+(1+m)x-2m=0,根据△≥0,即可解答.
③令函数值为0,求得(m-1)x2+(1+m)x-2m=0,解得x1=-1,x2=
| 2m |
| m-1 |
④根据特征数的特点,直接得出x的值,进一步验证即可解答.
解答:解:因为函数y=ax2+bx+c的特征数为[m-1,1+m,-2m];
①当m=3时,y=2x2+4x-6=2(x+1)2-8,顶点坐标是(-1,-8);此结论正确;
②令y=0,有(m-1)x2+(1+m)x-2m=0,因为△=(1+m)2-4(m-1)×(-2m)=(3m-1)2≥0,
所以函数图象与x轴始终有交点,此结论正确;
③当m>1时,令y=0,有(m-1)x2+(1+m)x-2m=0,解得,x1=-1,x2=
,
|x2-x1|=
>3,所以当m>1时,函数图象截x轴所得的线段长度大于3,此结论正确;
④经过定点,说明任意x代入,都不存在m,设m=2则x2+3x-2=0,即(x+2)(x-1)=0,即x=-2或1.当x=1时,y=(m-1)x2+(1+m)x-2m=0 即对任意m,函数图象都经过点(1,0)那么同样的:当x=-2时,y=(m-1)x2+(1+m)x-2m=-6即对任意m,函数图象都经过点(-2,-6),函数图象都经过两个点(1,0),(-2,-6),此结论正确.
根据上面的分析,①②③④都是正确的.
故答案为:①②③④.
①当m=3时,y=2x2+4x-6=2(x+1)2-8,顶点坐标是(-1,-8);此结论正确;
②令y=0,有(m-1)x2+(1+m)x-2m=0,因为△=(1+m)2-4(m-1)×(-2m)=(3m-1)2≥0,
所以函数图象与x轴始终有交点,此结论正确;
③当m>1时,令y=0,有(m-1)x2+(1+m)x-2m=0,解得,x1=-1,x2=
| 2m |
| m-1 |
|x2-x1|=
| 3m-1 |
| m-1 |
④经过定点,说明任意x代入,都不存在m,设m=2则x2+3x-2=0,即(x+2)(x-1)=0,即x=-2或1.当x=1时,y=(m-1)x2+(1+m)x-2m=0 即对任意m,函数图象都经过点(1,0)那么同样的:当x=-2时,y=(m-1)x2+(1+m)x-2m=-6即对任意m,函数图象都经过点(-2,-6),函数图象都经过两个点(1,0),(-2,-6),此结论正确.
根据上面的分析,①②③④都是正确的.
故答案为:①②③④.
点评:此题考查二次函数的性质,顶点坐标,抛物线与x轴的交点情况,两点间的距离公式,以及二次函数图象上点的坐标特征,熟练掌握二次函数的性质是和点的坐标特征是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
点M(5,3)关于x轴的对称点的坐标是( )
| A、(-5,-3) |
| B、(5,-3) |
| C、(-5,3) |
| D、(5,3) |
一天有8.64×104S,一年按365天计算,用科学记数法表示一年有多少秒的是( )
| A、3153.6×104S |
| B、3.65×104S |
| C、3.1536×107S |
| D、0.31536×104S |
 MN是一面长10m的墙,用长24m的篱笆,围成一个一面是墙,中间隔着一道篱笆的矩形花圃ABCD,已知花圃的设计面积为45m2,花圃的宽应当是多少?
MN是一面长10m的墙,用长24m的篱笆,围成一个一面是墙,中间隔着一道篱笆的矩形花圃ABCD,已知花圃的设计面积为45m2,花圃的宽应当是多少?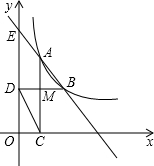 已知:如图,在平面直角坐标系中,直线AB与反比例函数y=
已知:如图,在平面直角坐标系中,直线AB与反比例函数y=