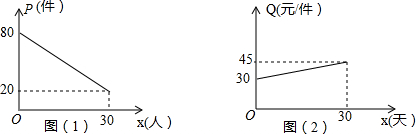题目内容
15. 如图,小手盖住的点的坐标可能是( )
如图,小手盖住的点的坐标可能是( )| A. | (3,3) | B. | (-4,5) | C. | (-4,-6) | D. | (3,-6) |
分析 根据盖住的点在第二象限,对各选项分析判断即可得解.
解答 解:A、(3,3)在第一象限;
B、(-4,5)在第二象限;
C、(-4,-6)在第三象限;
D、(3,-6)在第四象限.
故选B.
点评 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.观察如下所示规律排列的数组,{1},{2,3},{4,5,6},…,(从第二组开始,每组中数的个数都比前一组多一个),若假定某个数所在的组数为a,并且是这个组内的第b个数,那么2017这个数所对应的a、b分别为( )
| A. | 64,1 | B. | 63,62 | C. | 63,1 | D. | 63,63 |
5.某中学八年级(1)班数学课外兴趣小组在探究:“n边形共有多少条对角线”这一问题时,设计了如下表格:
(1)探究:假若你是该小组的成员,请把你研究的结果填入上表;
(2)猜想:随着边数的增加,多边形对角线的条数会越来越多,从n边形的一个顶点出发可引的对角线条数为(n-3)),n边形对角线的总条数为$\frac{n(n-3)}{2}$(n≥3).
(3)应用:10个人聚会,每不相邻的人都握一次手,共握多少次手?
| 多边形的边数 | 4 | 5 | 6 | 7 | 8 | … |
| 从多边形一个顶点出发可引起的对角线条数 | 1 | 2 | 3 | 4 | 5 | … |
| 多边形对角线的总条数 | 2 | 5 | 9 | 14 | 20 | … |
(2)猜想:随着边数的增加,多边形对角线的条数会越来越多,从n边形的一个顶点出发可引的对角线条数为(n-3)),n边形对角线的总条数为$\frac{n(n-3)}{2}$(n≥3).
(3)应用:10个人聚会,每不相邻的人都握一次手,共握多少次手?
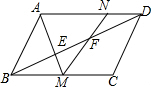 如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.
如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.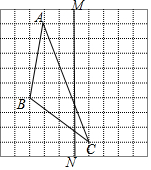 如图,在正方形网格上有一个△ABC.
如图,在正方形网格上有一个△ABC.