Question

3．在平面直角坐标系中，点C沿着某条路径运动，以点C为旋转中心，将点A（0，4）逆时针旋转90°到点B（m，1），若-5≤m≤5，则点C运动的路径长为5$\sqrt{2}$．

Answer 1

分析 在平面直角坐标系中，在y轴上取点P（0，1），过P作直线l∥x轴，作CM⊥OA于M，作CN⊥l于N，构造Rt△BCN≌Rt△ACM，得出CN=CM，若连接CP，则点C在∠BPO的平分线上，进而得出动点C在直线CP上运动；再分两种情况讨论C的路径端点坐标：①当m=-5时，②当m=5时，分别求得C（-1，0）和C₁（4，5），而C的运动路径长就是CC₁的长，最后由勾股定理可得CC₁的长度．

解答 解：如图1所示，在y轴上取点P（0，1），过P作直线l∥x轴，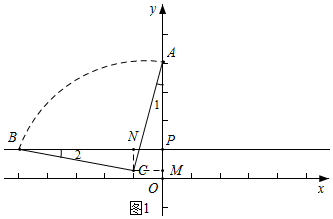

∵B（m，1），
∴B在直线l上，
∵C为旋转中心，旋转角为90°，
∴BC=AC，∠ACB=90°，
∵∠APB=90°，
∴∠1=∠2，
作CM⊥OA于M，作CN⊥l于N，则Rt△BCN≌Rt△ACM，
∴CN=CM，
若连接CP，则点C在∠BPO的平分线上，
∴动点C在直线CP上运动；
如图2所示，∵B（m，1）且-5≤m≤5，
∴分两种情况讨论C的路径端点坐标，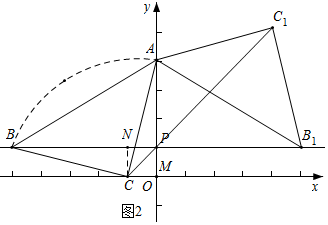

①当m=-5时，B（-5，1），PB=5，
作CM⊥y轴于M，作CN⊥l于N，
同理可得△BCN≌△ACM，
∴CM=CN，BN=AM，
可设PN=PM=CN=CM=a，
∵P（0，1），A（0，4），
∴AP=3，AM=BN=3+a，
∴PB=a+3+a=5，
∴a=1，
∴C（-1，0）；
②当m=5时，B（5，1），如图2中的B₁，此时的动点C是图2中的C₁，
同理可得C₁（4，5），
∴C的运动路径长就是CC₁的长，
由勾股定理可得，CC₁=$\sqrt{[4-（-1）]^{2}+{5}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$．

点评 本题主要考查了旋转图形的坐标、全等三角形的判定与性质以及轨迹的运用，解题时注意：图形或点旋转之后要结合旋转的角度和图形的特殊性质，求出旋转后的点的坐标．