Question

5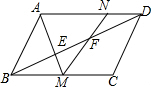．如图，平行四边形ABCD周长为40，∠ABC=60°，E，F在BD上，BE=EF=FD，AE的延长线交BC于M，MF的延长线交AD于N，设BC=x，△ANM的面积为y，求y关于x的函数解析式．

Answer 1

分析 根据平行四边形的性质得出AD∥BC，AD=BC=x，那么△BME∽△DAE，△BMF∽△DNF，由相似三角形对应边成比例求出BM=$\frac{1}{2}$AD=$\frac{1}{2}$x，DN=$\frac{1}{2}$BM=$\frac{1}{4}$x，那么AN=AD-DN=x-$\frac{1}{4}$x=$\frac{3}{4}$x．作AG⊥BC于G，解直角△ABG，求出AG=AB•sin∠ABG=$\frac{\sqrt{3}}{2}$（20-x），然后根据△ANM的面积=$\frac{1}{2}$AN•AG即可求解．

解答 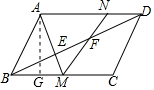解：∵四边形ABCD是平行四边形，BC=x，
∴AD∥BC，AD=BC=x，
∴△BME∽△DAE，△BMF∽△DNF，
又∵BE=EF=FD，
∴$\frac{BM}{DA}$=$\frac{BE}{DE}$=$\frac{1}{2}$，$\frac{BM}{DN}$=$\frac{BF}{DF}$=2，
∴BM=$\frac{1}{2}$AD=$\frac{1}{2}$x，DN=$\frac{1}{2}$BM=$\frac{1}{4}$x，
∴AN=AD-DN=x-$\frac{1}{4}$x=$\frac{3}{4}$x．
∵平行四边形ABCD周长为40，BC=x，
∴AB=CD=20-x．
如图，作AG⊥BC于G．
在△ABG中，∵∠AGB=90°，∠ABG=60°，AB=20-x，
∴AG=AB•sin∠ABG=$\frac{\sqrt{3}}{2}$（20-x），
∴△ANM的面积y=$\frac{1}{2}$AN•AG=$\frac{1}{2}$•$\frac{3}{4}$x•$\frac{\sqrt{3}}{2}$（20-x）=-$\frac{3\sqrt{3}}{16}$x²+$\frac{15\sqrt{3}}{4}$x，
即y关于x的函数解析式为y=-$\frac{3\sqrt{3}}{16}$x²+$\frac{15\sqrt{3}}{4}$x．

点评 本题考查了二次函数的应用，平行四边形的性质，解直角三角形，相似三角形的判定与性质，三角形的面积等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．