题目内容
20．
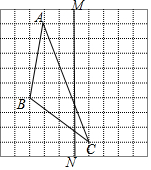如图，在正方形网格上有一个△ABC．（1）在图上画△ABC关于直线MN的对称图形（不写画法）；
（2）若网格上的每个小正方形的边长为2，直接写出△ABC的面积．
分析 （1）分别作出各点关于直线MN的对称点，再顺次连接即可；
（2）利用矩形的面积减去三个顶点上三角形的面积即可．
解答 
解：（1）如图所示，△A′B′C′即为所求；
（2）S△ABC=8×16-$\frac{1}{2}$×8×6-$\frac{1}{2}$×2×10-$\frac{1}{2}$×6×16=46．
点评 本题考查的是作图-轴对称变换，熟知轴对称的性质是解答此题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
10．
如图是二次函数y=ax2+bx+c的图象，下列结论：
①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为-2；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
如图是二次函数y=ax2+bx+c的图象，下列结论：①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为-2；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．
李老师用直尺和圆规作已知角的平分线．
作法：①以点O为圆心，适当长为半径画弧，交OA于点D，交OB于点E
②分别以点D、E为圆心，大于$\frac{1}{2}$DE的长为半径画弧，两弧在∠AOB的内部相交于点C．
③画射线OC，则OC就是∠AOB的平分线．
李老师用尺规作角平分线时，用到的三角形全等的判定方法是（ ）
李老师用直尺和圆规作已知角的平分线．作法：①以点O为圆心，适当长为半径画弧，交OA于点D，交OB于点E
②分别以点D、E为圆心，大于$\frac{1}{2}$DE的长为半径画弧，两弧在∠AOB的内部相交于点C．
③画射线OC，则OC就是∠AOB的平分线．
李老师用尺规作角平分线时，用到的三角形全等的判定方法是（ ）
| A． | SSS | B． | SAS | C． | ASA | D． | AAS |
15．
如图，小手盖住的点的坐标可能是（ ）
如图，小手盖住的点的坐标可能是（ ）| A． | （3，3） | B． | （-4，5） | C． | （-4，-6） | D． | （3，-6） |
