题目内容
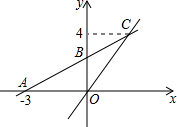 如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=
如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=| 4 |
| 3 |
(1)求一次函数y=kx+b的解析式;
(2)D是平面内一点,以O、C、D、B四点为顶点的四边形是平行四边形,直接写出点D的坐标.(不必写出推理过程).
考点:两条直线相交或平行问题,平行四边形的性质
专题:
分析:(1)先把点C的坐标代入正比例函数关系式,可求出m的值,再把点A,C的坐标代入一次函数的解析式求出k,b即可.
(2)利用CD平行且等于AO求解.
(2)利用CD平行且等于AO求解.
解答:解:(1)把点C(m,4),代入正比例函数y=
x得,
4=
m,解得m=3,
∴点C的坐标为(3,4),
∵A的坐标为(-3,0)
∴
解得
∴一次函数的解析式为:y=
x+2.
(2)∵O、C、D、B四点为顶点的四边形是平行四边形,
∴只要CD平行且等于AO,即CD=3,
①当点D在点C的左边时,点D的坐标为(0,4),
②当点D在点C的右边时,点D的坐标为(6,4),
∴点D的坐标为(0,4)或(6,4),
| 4 |
| 3 |
4=
| 4 |
| 3 |
∴点C的坐标为(3,4),
∵A的坐标为(-3,0)
∴
|
解得
|
∴一次函数的解析式为:y=
| 2 |
| 3 |
(2)∵O、C、D、B四点为顶点的四边形是平行四边形,
∴只要CD平行且等于AO,即CD=3,
①当点D在点C的左边时,点D的坐标为(0,4),
②当点D在点C的右边时,点D的坐标为(6,4),
∴点D的坐标为(0,4)或(6,4),
点评:本题主要考查了两直线相交平行问题及平行四边形的判定,解题的关键是求出一次函数的解析式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如果关于x、y的方程组
的解是正数,那么a的取值范围是( )
|
A、-2<a<
| ||
B、a>-
| ||
| C、a<2 | ||
D、a<-
|
 如图,抛物线y=ax2+bx-3a(a≠0)与x轴交于点A(-1,0)和点B,与y轴交于点C(0,2),连接BC.
如图,抛物线y=ax2+bx-3a(a≠0)与x轴交于点A(-1,0)和点B,与y轴交于点C(0,2),连接BC.
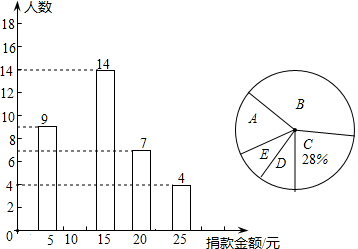 某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.
某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.