题目内容
已知:在正方形ABCD中,E、G分别是射线CB、DA上的两个动点,点F是CD边上,满足EG⊥BF,
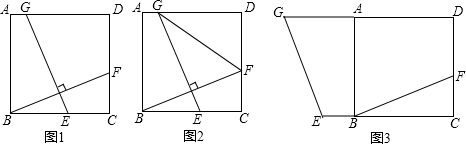
(1)如图1,当E、G在CB、DA边上运动时(不与正方形顶点重合),求证:GE=BF.
(2)如图2,在(1)的情况下,连结GF,求证:FG+BE>
BF.
(3)如图3,当E、G运动到BC、AD的反向延长线时,请你直接写出FG、BE、BF三者的数量关系(不必写出证明过程).

(1)如图1,当E、G在CB、DA边上运动时(不与正方形顶点重合),求证:GE=BF.
(2)如图2,在(1)的情况下,连结GF,求证:FG+BE>
| 2 |
(3)如图3,当E、G运动到BC、AD的反向延长线时,请你直接写出FG、BE、BF三者的数量关系(不必写出证明过程).
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)过点G作GH⊥BC于H,可得四边形ABHG是矩形,根据矩形的对边相等可得AB=GH,再求出BC=GH,然后根据同角的余角相等可得∠CBF=∠HGE,然后根据“角边角”证明△BCF和△GHE全等,根据全等三角形对应边相等可得GE=BF;
(2)把△BCF绕点B逆时针旋转90°得到△BAH,连接HF,可得△BFH是等腰直角三角形,根据等腰直角三角形的性质可得HF=
BF,根据旋转的性质可得BH=BF,再根据垂直于同一直线的两直线互相平行可得BH∥GE,然后求出四边形BEGH是平行四边形,根据平行四边形的对边相等可得GH=BE,然后利用三角形的任意两边之和大于第三边证明即可;
(3)证明方法同(2).
(2)把△BCF绕点B逆时针旋转90°得到△BAH,连接HF,可得△BFH是等腰直角三角形,根据等腰直角三角形的性质可得HF=
| 2 |
(3)证明方法同(2).
解答: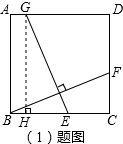 (1)证明:如图,过点G作GH⊥BC于H,
(1)证明:如图,过点G作GH⊥BC于H,
则四边形ABHG是矩形,
∴AB=GH,
∵四边形ABCD是正方形,
∴AB=BC,
∴BC=GH,
∵EG⊥BF,
∴∠CBF+∠BEG=∠HGE+∠BEG=90°,
∴∠CBF=∠HGE,
在△BCF和△GHE中,
,
∴△BCF≌△GHE(ASA),
∴GE=BF;
(2)证明:如图,把△BCF绕点B逆时针旋转90°得到△BAH,连接HF,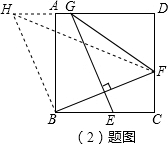
则△BFH是等腰直角三角形,
∴HF=
BF,
由旋转的性质得,BH=BF,
∵BF=GE,
∴BH=GE,
∵EG⊥BF,∠HBF=90°,
∴BH∥GE,
∴四边形BEGH是平行四边形,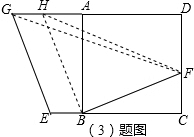
∴GH=BE,
在△GHF中,FG+GH>HF,
∴FG+BE>
BF;
(3)解:如图,同(2)可得GH=BE,HF=
BF,
在△GHF中,HF+GH>FG,
∴
BF+BE>FG.
 (1)证明:如图,过点G作GH⊥BC于H,
(1)证明:如图,过点G作GH⊥BC于H,则四边形ABHG是矩形,
∴AB=GH,
∵四边形ABCD是正方形,
∴AB=BC,
∴BC=GH,
∵EG⊥BF,
∴∠CBF+∠BEG=∠HGE+∠BEG=90°,
∴∠CBF=∠HGE,
在△BCF和△GHE中,
|
∴△BCF≌△GHE(ASA),
∴GE=BF;
(2)证明:如图,把△BCF绕点B逆时针旋转90°得到△BAH,连接HF,

则△BFH是等腰直角三角形,
∴HF=
| 2 |
由旋转的性质得,BH=BF,
∵BF=GE,
∴BH=GE,
∵EG⊥BF,∠HBF=90°,
∴BH∥GE,
∴四边形BEGH是平行四边形,

∴GH=BE,
在△GHF中,FG+GH>HF,
∴FG+BE>
| 2 |
(3)解:如图,同(2)可得GH=BE,HF=
| 2 |
在△GHF中,HF+GH>FG,
∴
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的性质,三角形的任意两边之和大于第三边,平行四边形的判定与性质,熟记各性质并作辅助线构造出全等三角形和平行四边形是解题的关键.

练习册系列答案
相关题目
随着通讯市场竞争日益激烈,某通讯公司的手机市话费标准按原价标准每分钟降低a元后,再次下调25%,现在的收费标准是每分钟b元,则收费标准是每分钟( )
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
下列各点中,在函数y=-
图象上的是( )
| 6 |
| x |
| A、(-2,-4) | ||
| B、(2,3) | ||
| C、(-1,6) | ||
D、(-
|
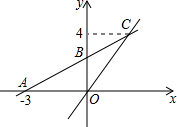 如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=
如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=