题目内容
先化简，再求值：（a-2）2+（1-a）（1+a），其中a=
．
| 3 |
| 4 |
考点：整式的混合运算—化简求值
专题：
分析：先算乘法，再合并同类项，最后代入求出即可．
解答：解：（a-2）2+（1-a）（1+a）
=a2-4a+4+1-a2
=-4a+5，
当a=
时，原式=-4×
+5=2．
=a2-4a+4+1-a2
=-4a+5，
当a=
| 3 |
| 4 |
| 3 |
| 4 |
点评：本题考查了整式的混合运算和求值的应用，主要考查学生的计算和化简能力，题目比较好，难度适中．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
如图，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2014厘米后停下，则这只蚂蚁停在下列命题中，不正确的是（ ）
| A、在同一平面内，过一点有而且只有一条直线与已知直线垂直 |
| B、经过直线外一点，有而且只有一条直线与这条直线平行 |
| C、垂直于同一直线的两条直线垂直 |
| D、平行于同一直线的两条直线平行 |
在△ABC和△A′B′C′中A′B′=AB，∠B=∠B′，补充条件后仍不一定能保证△A′B′C′≌△ABC，则补充的条件是（ ）
| A、A′C′=AC |
| B、B′C′=BC |
| C、∠A′=∠A |
| D、∠C′=∠C |
下列各点中，在函数y=-
图象上的是（ ）
| 6 |
| x |
| A、（-2，-4） | ||
| B、（2，3） | ||
| C、（-1，6） | ||
D、（-
|
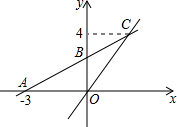如图，在平面直角坐标系xOy中，O是坐标原点，一次函数y=kx+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数y=