题目内容
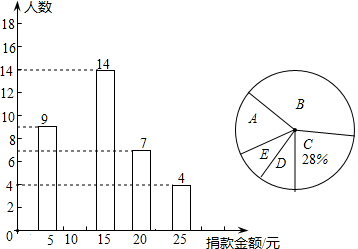 某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.
某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.A.捐款5元
B.捐款10元
C.捐款15元
D.捐款20元
E.捐款25元
(1)求该班的总人数,并将条形图补充完整;
(2)写出每人捐款数的众数和中位数;
(3)该班平均每人捐款多少元?
(4)在活动总结班会上,计划在捐款最多的E组中找两名同学代表发言,如果E组中有2名男生,那么选中的两名同学正好是一名男生一名女生的概率是多少?
考点:条形统计图,扇形统计图,中位数,众数,列表法与树状图法
专题:
分析:(1)用捐款15元的人数14除以所占的百分比28%,计算即可得解,用该班总人数减去其它四种捐款额的人数,计算即可求出捐款10元的人数,然后补全条形统计图;
(2)根据找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.根据众数的定义,人数最多即为捐款总额的众数;
(3)根据加权平均数的求解方法列式计算即可得解;
(4)先列出表格,再根据概率的求法即可求解.
(2)根据找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.根据众数的定义,人数最多即为捐款总额的众数;
(3)根据加权平均数的求解方法列式计算即可得解;
(4)先列出表格,再根据概率的求法即可求解.
解答:解:(1)14÷28%=50(人).
该班总人数为50人;
捐款10元的人数:50-9-14-7-4=50-34=16,
图形补充如图所示:

(2)众数是10,
中位数是(10+15)÷2=12.5;
(3)
×(5×9+10×16+15×14+20×7+25×4)
=
×655
=13.1元,
因此该班平均每人捐款13.1元.
(4)列表如下:
E组中有2名男生,2名女生,
共有12种可能,选中的两名同学正好是1名男生1名女生的概率是
=
.
该班总人数为50人;
捐款10元的人数:50-9-14-7-4=50-34=16,
图形补充如图所示:

(2)众数是10,
中位数是(10+15)÷2=12.5;
(3)
| 1 |
| 50 |
=
| 1 |
| 50 |
=13.1元,
因此该班平均每人捐款13.1元.
(4)列表如下:
| 男1 | 男2 | 女1 | 女2 | |
| 男1 | √ | √ | ||
| 男2 | √ | √ | ||
| 女1 | √ | √ | ||
| 女2 | √ | √ |
共有12种可能,选中的两名同学正好是1名男生1名女生的概率是
| 8 |
| 12 |
| 2 |
| 3 |
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
下列命题中,不正确的是( )
| A、在同一平面内,过一点有而且只有一条直线与已知直线垂直 |
| B、经过直线外一点,有而且只有一条直线与这条直线平行 |
| C、垂直于同一直线的两条直线垂直 |
| D、平行于同一直线的两条直线平行 |
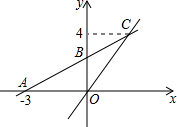 如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=
如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=