题目内容
如果关于x、y的方程组
的解是正数，那么a的取值范围是（ ）
|
A、-2＜a＜
| ||
B、a＞-
| ||
| C、a＜2 | ||
D、a＜-
|
考点：二元一次方程组的解,解一元一次不等式组
专题：计算题
分析：将a看做已知数求出方程组的解表示出x与y，根据x与y都为正数，取出a的范围即可．
解答：解：
，
①×2+②得：5x=2a+4，即x=
，
将x=
代入①得：y=
-a，
根据题意得：
，
解得：-2＜a＜
．
故选A
|
①×2+②得：5x=2a+4，即x=
| 2a+4 |
| 5 |
将x=
| 2a+4 |
| 5 |
| 2a+4 |
| 5 |
根据题意得：
|
解得：-2＜a＜
| 4 |
| 3 |
故选A
点评：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．
练习册系列答案
相关题目
随着通讯市场竞争日益激烈，某通讯公司的手机市话费标准按原价标准每分钟降低a元后，再次下调25%，现在的收费标准是每分钟b元，则收费标准是每分钟（ ）
A、（
| ||
B、（
| ||
C、（
| ||
D、（
|
下列命题中，不正确的是（ ）
| A、在同一平面内，过一点有而且只有一条直线与已知直线垂直 |
| B、经过直线外一点，有而且只有一条直线与这条直线平行 |
| C、垂直于同一直线的两条直线垂直 |
| D、平行于同一直线的两条直线平行 |
下列命题：
①同旁内角互补，两直线平行；
②同位角相等；
③直角都相等；
④相等的角是对顶角．
它们是真命题的个数是（ ）
①同旁内角互补，两直线平行；
②同位角相等；
③直角都相等；
④相等的角是对顶角．
它们是真命题的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC和△A′B′C′中A′B′=AB，∠B=∠B′，补充条件后仍不一定能保证△A′B′C′≌△ABC，则补充的条件是（ ）
| A、A′C′=AC |
| B、B′C′=BC |
| C、∠A′=∠A |
| D、∠C′=∠C |
下列各点中，在函数y=-
图象上的是（ ）
| 6 |
| x |
| A、（-2，-4） | ||
| B、（2，3） | ||
| C、（-1，6） | ||
D、（-
|
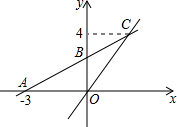如图，在平面直角坐标系xOy中，O是坐标原点，一次函数y=kx+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数y=