题目内容
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.请你回答下列问题:
(1)计算两班的优秀率.
(2)求两班比赛成绩的中位数.
(3)估计两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
(1)计算两班的优秀率.
(2)求两班比赛成绩的中位数.
(3)估计两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的由.
考点:方差,统计表,中位数
专题:计算题
分析:(1)根据统计表得到甲班有2个优秀,乙班有3个优秀,然后根据百分比的意义求解;
(2)先把两组数据由小到大排列,然后根据中位数的定义求解;
(3)比较两组数据,得到甲班的成绩波动比乙班的波动大,根据方差的意义得到乙的方差小;
(4)根据优秀率、中位数和方差的意义比较两班的成绩.
(2)先把两组数据由小到大排列,然后根据中位数的定义求解;
(3)比较两组数据,得到甲班的成绩波动比乙班的波动大,根据方差的意义得到乙的方差小;
(4)根据优秀率、中位数和方差的意义比较两班的成绩.
解答:解:(1)甲班的优秀率=
=40%;乙班的优秀率=
=60%;
(2)甲班的5名学生的比赛成绩由小到大排列为89,96,97,100,118,所以甲班的成绩的中位数为97;
乙班的5名学生的比赛成绩由小到大排列为91,95,100,104,110,所以乙班的成绩的中位数为100;
(3)由于甲班的成绩波动比乙班的波动大,所以可估计乙的方差小;
(4)因为乙班的优秀率比甲班大,乙班的中位数比甲班大,且乙班的方差比甲班小,所以乙班的成绩比甲班好,所以把冠军奖状发给甲班.
| 2 |
| 5 |
| 3 |
| 5 |
(2)甲班的5名学生的比赛成绩由小到大排列为89,96,97,100,118,所以甲班的成绩的中位数为97;
乙班的5名学生的比赛成绩由小到大排列为91,95,100,104,110,所以乙班的成绩的中位数为100;
(3)由于甲班的成绩波动比乙班的波动大,所以可估计乙的方差小;
(4)因为乙班的优秀率比甲班大,乙班的中位数比甲班大,且乙班的方差比甲班小,所以乙班的成绩比甲班好,所以把冠军奖状发给甲班.
点评:本题考查了方差:方差公式为s2=
[(x1-x?)2+(x2-x?)2+…+(xn-x?)2];方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了中位数.
| 1 |
| n |

练习册系列答案
相关题目
下列命题:
①同旁内角互补,两直线平行;
②同位角相等;
③直角都相等;
④相等的角是对顶角.
它们是真命题的个数是( )
①同旁内角互补,两直线平行;
②同位角相等;
③直角都相等;
④相等的角是对顶角.
它们是真命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各点中,在函数y=-
图象上的是( )
| 6 |
| x |
| A、(-2,-4) | ||
| B、(2,3) | ||
| C、(-1,6) | ||
D、(-
|

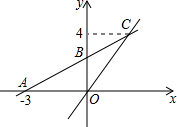 如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=
如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=