题目内容

20．（1）解方程：$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1
（2）解不等式组：$\left\{\begin{array}{l}{2（x-2）≤4x-3}\\{2x-5＜1-x}\end{array}\right.$．

分析 （1）方程两边都乘以x-3，化分式方程为整式方程，解整式方程求得x的值，再检验即可；
（2）分别求出每一个不等式的解集，根据口诀：大小小大中间找，确定不等式组的解集．

解答 解：（1）去分母得2-x-1=x-3．
解得：x=2，
经检验，x=2都是原方程的根．
（2）解不等式2（x-2）≤4x-3，得：x≥-$\frac{1}{2}$；
解不等式2x-5＜1-x，得 x＜2；
∴此不等式组的解集为：-$\frac{1}{2}$≤x＜2．

点评 本题主要考查解分式方程和不等式组的能力，熟练掌握解方程和不等式的基本步骤是关键．

练习册系列答案
相关题目
10．若（x-3）2+（3y+1）2=0，则x2016•y2017=-$\frac{1}{3}$．
11．计算：
（1）$\frac{1}{{\sqrt{3}+1}}-\frac{{\sqrt{3}}}{2}+\sqrt{32}×\sqrt{\frac{1}{8}}$
（2）$（\sqrt{3}+3\sqrt{2}-\sqrt{6}）（\sqrt{3}-\sqrt{6}-3\sqrt{2}）$．
8．计算：（-$\frac{1}{2}$）-2-（π-2016）0+sin45°+|1-$\sqrt{2}$|
15．先化简，再求值：
（1）先化简，再求值：a（a-4）-（a+6）（a-2），其中a=-$\frac{1}{2}$．
（2）先化简，再求值：（x+2y）（x-2y）-（2x-y）（-2x-y），其中x=8，y=-8；．
5．已知方程组$\left\{\begin{array}{l}2x+y=1\\ x+2y=k-2\end{array}$的解满足x-y=2，则k的值是1．
12．计算
（1）a-1-$\frac{a^2}{a+1}$
（2）先化简，再求值：$\frac{1}{x-1}-\frac{2}{{{x^2}-1}}$，其中x=2$\sqrt{2}$-1．
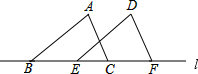9．已知△ABC的边在直线l上，BC=5，现把△ABC沿着直线l向右平移到△DEF的位置（如图所示），若EC=3，则△ABC平移的距离为（　　）
A．2B．3C．5D．7
10．解下列方程  
（1）$\frac{x-2}{x+2}-\frac{12}{{{x^2}-4}}=1$
（2）$\frac{y-2}{y-3}=2-\frac{1}{3-y}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网