题目内容
α、β是关于x的方程4x2-4mx+m2+4m=0的两个实根,并且满足(α-1)(β-1)-1=
,求m的值.
| 9 |
| 100 |
考点:根与系数的关系,根的判别式
专题:
分析:先根据一元二次方程根与系数的关系求出α+β与αβ,再代入(α-1)(β-1)-1=
求出m的值,然后用根的判别式进行检验.
| 9 |
| 100 |
解答:解∵α、β是关于x的方程4x2-4mx+m2+4m=0的两个实根,
∴α+β=m,αβ=
,
∵(α-1)(β-1)-1=
,
∴αβ-(α+β)+1-1=
,
即:
-m=
,
化简得:m2=
,
故m=±
,
又△=16m2-16m2-16m≥0,解得:m≤0,
故m=-
.
∴α+β=m,αβ=
| m2+4m |
| 4 |
∵(α-1)(β-1)-1=
| 9 |
| 100 |
∴αβ-(α+β)+1-1=
| 9 |
| 100 |
即:
| m2+4m |
| 4 |
| 9 |
| 100 |
化简得:m2=
| 9 |
| 25 |
故m=±
| 3 |
| 5 |
又△=16m2-16m2-16m≥0,解得:m≤0,
故m=-
| 3 |
| 5 |
点评:本题考查了根的判别式,根与系数的关系,属于基础题,关键是要熟记x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,有两个可以自由转动的转盘(每个转盘均被等分),同时转动这两个转盘,待转盘停止后,两个指针同时指在偶数上的概率是( )
如图,有两个可以自由转动的转盘(每个转盘均被等分),同时转动这两个转盘,待转盘停止后,两个指针同时指在偶数上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,要测量一幢楼CD的高度,在地面上A点测得楼CD的顶部C的仰角为30°,向楼前进50m到达B点,又测得点C的仰角为60°,求这幢楼CD的高度(结果保留根号)
如图,要测量一幢楼CD的高度,在地面上A点测得楼CD的顶部C的仰角为30°,向楼前进50m到达B点,又测得点C的仰角为60°,求这幢楼CD的高度(结果保留根号) 已知:(如图)边长为1的正方形ABCD内接于⊙O,点L为劣弧CD(不含端点)上任意一点.直线AL交线段CD于点K,直线CL交直线AD于点M,直线MK交线段BC于点N,线段LB交线段KN于点P.
已知:(如图)边长为1的正方形ABCD内接于⊙O,点L为劣弧CD(不含端点)上任意一点.直线AL交线段CD于点K,直线CL交直线AD于点M,直线MK交线段BC于点N,线段LB交线段KN于点P.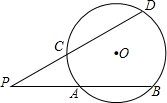 已知,顶点在圆上,并且两边都和圆相交的角叫圆周角.因为一条弧所对的圆周角等于它所对的弧的度数,所以圆周角的度数等于它所对的弧的度数的一半.类似的,有定义:顶点在圆外,并且两边都和圆相交的角叫圆外角.如图所示,∠DPB是圆外角,那么∠DPB的度数与它所夹的两段
已知,顶点在圆上,并且两边都和圆相交的角叫圆周角.因为一条弧所对的圆周角等于它所对的弧的度数,所以圆周角的度数等于它所对的弧的度数的一半.类似的,有定义:顶点在圆外,并且两边都和圆相交的角叫圆外角.如图所示,∠DPB是圆外角,那么∠DPB的度数与它所夹的两段
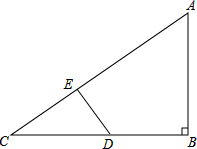 如图,∠B=90°,AB=6,BC=8,DE⊥AC交BC于点D,交AC于点E.设CD的长为x,四边形AEDB面积为y.
如图,∠B=90°,AB=6,BC=8,DE⊥AC交BC于点D,交AC于点E.设CD的长为x,四边形AEDB面积为y. 如图,矩形ABCD中,AB=8厘米,BC=12厘米,P、Q分别是AB、BC上运动的两点.若点P从点A出发,以1厘米/秒的速度沿AB方向运动,同时,点Q从点B出发以2厘米/秒的速度沿BC方向运动,设点P,Q运动的时间为x秒.
如图,矩形ABCD中,AB=8厘米,BC=12厘米,P、Q分别是AB、BC上运动的两点.若点P从点A出发,以1厘米/秒的速度沿AB方向运动,同时,点Q从点B出发以2厘米/秒的速度沿BC方向运动,设点P,Q运动的时间为x秒.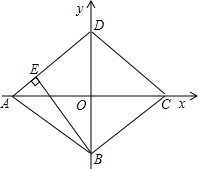 已知直角坐标系中菱形ABCD的位置如图,且C(4,0)、D(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
已知直角坐标系中菱形ABCD的位置如图,且C(4,0)、D(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.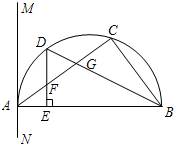 如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是
如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是