题目内容
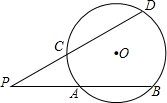 已知,顶点在圆上,并且两边都和圆相交的角叫圆周角.因为一条弧所对的圆周角等于它所对的弧的度数,所以圆周角的度数等于它所对的弧的度数的一半.类似的,有定义:顶点在圆外,并且两边都和圆相交的角叫圆外角.如图所示,∠DPB是圆外角,那么∠DPB的度数与它所夹的两段
已知,顶点在圆上,并且两边都和圆相交的角叫圆周角.因为一条弧所对的圆周角等于它所对的弧的度数,所以圆周角的度数等于它所对的弧的度数的一半.类似的,有定义:顶点在圆外,并且两边都和圆相交的角叫圆外角.如图所示,∠DPB是圆外角,那么∠DPB的度数与它所夹的两段 |
| BD |
 |
| AC |
(1)你的结论用文字表述为(不准出现字母和数学符号):
(2)证明你的结论.
考点:圆周角定理
专题:阅读型
分析:(1)圆外角的度数等于它所夹的弧的度数的差的绝对值的一半;
(2)连接DA,OA,OB,OC,OD,根据圆周角定理进行分析即可.
(2)连接DA,OA,OB,OC,OD,根据圆周角定理进行分析即可.
解答:解:(1)圆外角的度数等于它所夹的弧的度数的差的绝对值的一半 ;
;
(2)连接DA,OA,OB,OC,OD
∵
的度数=∠BOD的度数,
的度数=∠AOC的度数,
∠BAD=
∠BOD,∠ADC=
∠AOC
∴∠BAD-∠ADC=
∠BOD-
∠AOC,
∵∠DPB=∠BAD-∠ADC;
∴∠DPB=
∠BOD-
∠AOC=
(∠BOD-∠AOC),
∵
的度数=∠BOD的度数,
的度数=∠AOC的度数,
∴∠DPB的度数=
(∠BOD的度数-∠AOC的度数);
 ;
;(2)连接DA,OA,OB,OC,OD
∵
 |
| BD |
 |
| AC |
∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BAD-∠ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DPB=∠BAD-∠ADC;
∴∠DPB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵
 |
| BD |
 |
| AC |
∴∠DPB的度数=
| 1 |
| 2 |
点评:本题是对圆周角定理的拓展,利用了圆周角定理来求解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目

 如图,在矩形ABCD中,AB=2,AD=4,点P在AD上且AP=1.将一块三角尺顶点放在点P处,三角尺的两直角边分别交AB、BC于点E、F.
如图,在矩形ABCD中,AB=2,AD=4,点P在AD上且AP=1.将一块三角尺顶点放在点P处,三角尺的两直角边分别交AB、BC于点E、F. 如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E,求∠E的度数.
如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E,求∠E的度数.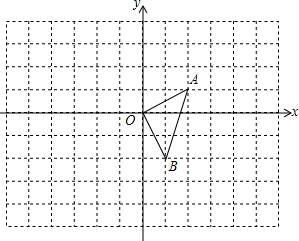 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).