题目内容
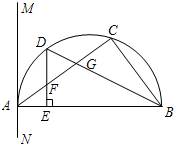 如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是
如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是 |
| AC |
(1)请说明MN是半圆的切线;
(2)请说明FD=FG;
(3)若△DFG的面积为9,且DG:GC=3:4,试求△BCG的面积.
考点:圆的综合题,等腰三角形的判定,圆周角定理,切线的判定,相似三角形的判定与性质
专题:综合题
分析:(1)如图1,由AB是半圆的直径可得∠ACB=90°,从而有∠CAB+∠ABC=90°,再结合条件∠MAC=∠ABC就可证到∠MAB=90°,进而可证到MN是半圆的切线.
(2)连接AD,如图2,由D是
的中点可得∠DAC=∠DBA,由DE⊥AB,∠ADB=90°可得∠ADE=∠DBA,从而有∠DAC=∠ADE;再根据∠ADB=90°就可证到∠EDB=∠DGA,则有FD=FG.
(3)如图2,由FA=FD,FD=FG可得FA=FG,由条件“△DFG的面积为9”就可求出△ADG的面积;易证△ADG∽△BCG,根据相似三角形的面积比等于相似比的平方即可求出△BCG的面积.
(2)连接AD,如图2,由D是
 |
| AC |
(3)如图2,由FA=FD,FD=FG可得FA=FG,由条件“△DFG的面积为9”就可求出△ADG的面积;易证△ADG∽△BCG,根据相似三角形的面积比等于相似比的平方即可求出△BCG的面积.
解答:解:(1)如图1,
∵AB是半圆的直径,
∴∠ACB=90°.
∴∠CAB+∠ABC=90°.
∵∠MAC=∠ABC,
∴∠CAB+∠MAC=90°.
∴∠MAB=90°,即MA⊥AB.
∵MA经过直径AB的外端,且MA⊥AB,
∴MN是半圆的切线.
(2)连接AD,如图2.
∵D是
的中点,
∴∠DAC=∠DBA.
∵DE⊥AB,∠ADB=90°,
∴∠ADE=90°-∠EDB=∠DBA.
∴∠DAC=∠ADE.
∴FA=FD.
∵∠ADB=90°,
∴∠ADE+∠EDB=90°,∠DAC+∠DGA=90°.
∴∠EDB=∠DGA.
∴FD=FG.
(3)如图2,
∵FA=FD,FD=FG,
∴FA=FG.
∴AG=2FG.
∴S△ADG=2S△FDG=18.
∵∠DAG=∠CBG,∠AGD=∠BGC,
∴△ADG∽△BCG.
∴
=(
)2.
∵DG:GC=3:4,S△ADG=18.
∴
=
.
∴S△BCG=32.
∴△BCG的面积为32.

∵AB是半圆的直径,
∴∠ACB=90°.
∴∠CAB+∠ABC=90°.
∵∠MAC=∠ABC,
∴∠CAB+∠MAC=90°.
∴∠MAB=90°,即MA⊥AB.
∵MA经过直径AB的外端,且MA⊥AB,
∴MN是半圆的切线.
(2)连接AD,如图2.
∵D是
 |
| AC |
∴∠DAC=∠DBA.
∵DE⊥AB,∠ADB=90°,
∴∠ADE=90°-∠EDB=∠DBA.
∴∠DAC=∠ADE.
∴FA=FD.

∵∠ADB=90°,
∴∠ADE+∠EDB=90°,∠DAC+∠DGA=90°.
∴∠EDB=∠DGA.
∴FD=FG.
(3)如图2,
∵FA=FD,FD=FG,
∴FA=FG.
∴AG=2FG.
∴S△ADG=2S△FDG=18.
∵∠DAG=∠CBG,∠AGD=∠BGC,
∴△ADG∽△BCG.
∴
| S△ADG |
| S△BCG |
| DG |
| CG |
∵DG:GC=3:4,S△ADG=18.
∴
| 18 |
| S△BCG |
| 9 |
| 16 |
∴S△BCG=32.
∴△BCG的面积为32.
点评:本题主要考查了切线的判定、圆周角定理、等腰三角形的判定、相似三角形的判定与性质等知识,有一定的综合性,而证出FA=FG及运用相似三角形的性质(相似三角形的面积比等于相似比的平方)是解决第(3)小题的关键.

练习册系列答案
相关题目

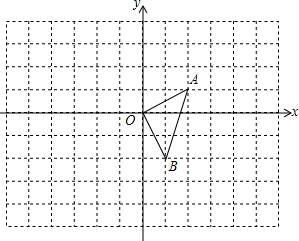 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).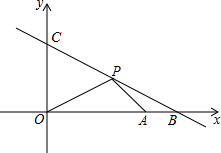 在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.
在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.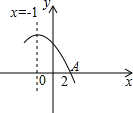 已知二次函数y=ax2+bx+c的部分图象如图,其对称轴为直线x=-1.若其与x轴的一个交点为A(2,0),则由图象可知,当自变量x的取值范围是
已知二次函数y=ax2+bx+c的部分图象如图,其对称轴为直线x=-1.若其与x轴的一个交点为A(2,0),则由图象可知,当自变量x的取值范围是