题目内容
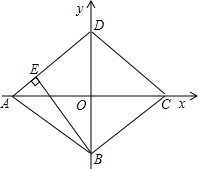 已知直角坐标系中菱形ABCD的位置如图,且C(4,0)、D(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
已知直角坐标系中菱形ABCD的位置如图,且C(4,0)、D(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.(1)填空:菱形ABCD的边长是
(2)若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值.
考点:菱形的性质,相似三角形的判定与性质
专题:
分析:(1)根据点C、D的坐标求出OC、OD,然后利用勾股定理列式计算即可求出边长,根据菱形的对角线互相垂直平分求出AC、BD,再根据菱形的面积等于对角线乘积的一半列式计算即可得解;利用菱形的面积列出方程求解即可得到BE的长;
(2)过点Q作QG⊥AD,垂足为G,根据△AQG和△ABE相似,利用相似三角形对应边成比例列式表示出QG,然后根据三角形的面积公式列式整理即可,再根据二次函数的最值问题解答,
(2)过点Q作QG⊥AD,垂足为G,根据△AQG和△ABE相似,利用相似三角形对应边成比例列式表示出QG,然后根据三角形的面积公式列式整理即可,再根据二次函数的最值问题解答,
解答: 解:(1)∵C(4,0)、D(0,3),
解:(1)∵C(4,0)、D(0,3),
∴OC=4,OD=3,
由勾股定理得,CD=
=
=5,
∵AC=2OC=8,BD=2OD=6,
∴菱形的面积=
×8×6=24,
菱形的面积=
×5BE=24,
解得BE=
;
故答案为:5,24,
;
(2)由题意,得AP=t,AQ=10-2t,
如图,过点Q作QG⊥AD,垂足为G,
∵QG∥BE,
∴△AQG∽△ABE,
∴
=
,
∴QG=
×
=
-
t,
∴S=
AP•QG=
t(
-
t)=-
t2+
t(
≤t≤5),
∵S=-
t2+
t=-
(t-
)2+6(
≤t≤5)
∴当t=
时,S最大值为6.
 解:(1)∵C(4,0)、D(0,3),
解:(1)∵C(4,0)、D(0,3),∴OC=4,OD=3,
由勾股定理得,CD=
| OC2+OD2 |
| 42+32 |
∵AC=2OC=8,BD=2OD=6,
∴菱形的面积=
| 1 |
| 2 |
菱形的面积=
| 1 |
| 2 |
解得BE=
| 24 |
| 5 |
故答案为:5,24,
| 24 |
| 5 |
(2)由题意,得AP=t,AQ=10-2t,
如图,过点Q作QG⊥AD,垂足为G,
∵QG∥BE,
∴△AQG∽△ABE,
∴
| QG |
| BE |
| AQ |
| AB |
∴QG=
| 10-2t |
| 5 |
| 24 |
| 5 |
| 48 |
| 5 |
| 48 |
| 25 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 48 |
| 5 |
| 48 |
| 25 |
| 24 |
| 25 |
| 24 |
| 5 |
| 5 |
| 2 |
∵S=-
| 24 |
| 25 |
| 24 |
| 5 |
| 24 |
| 25 |
| 5 |
| 2 |
| 5 |
| 2 |
∴当t=
| 5 |
| 2 |
点评:本题考查了菱形的性质,相似三角形的判定与性质,勾股定理,二次函数的应用,(1)利用菱形的面积列出方程是求BE的关键,(2)求面积的最大值时要注意t的取值范围.

练习册系列答案
相关题目
 已知:点A、B、C在同一直线上,BC=
已知:点A、B、C在同一直线上,BC= 已知:如图,在直角坐标系xOy中,点A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
已知:如图,在直角坐标系xOy中,点A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D. 如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E,求∠E的度数.
如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E,求∠E的度数.

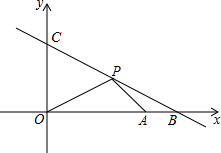 在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.
在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.