题目内容
如图,在平面直角坐标系中,以CD为弦的⊙P交y轴于点A、B,已知A、C、D三点的坐标分别为A(0,-8)、C(-4,0)、D(4,0).
(1)求⊙P的半径;
(2)如图2,连接DP并延长交⊙P于E,点Q是直径DE上的一个动点,求OQ的长的取值范围.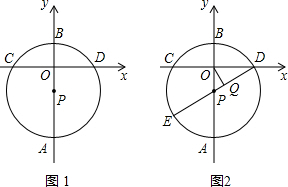
(1)求⊙P的半径;
(2)如图2,连接DP并延长交⊙P于E,点Q是直径DE上的一个动点,求OQ的长的取值范围.

考点:圆的综合题
专题:综合题
分析:(1)连接PD,设⊙P的半径为r,根据坐标与图形性质得OC=OD=4,OA=8,在Rt△ODP中,根据勾股定理得(8-r)2+42=r2,然后解方程即可得到⊙P的半径;
(2作OQ′⊥DE于Q′,连接OE,如图2,先利用面积法计算出OQ′=
,接着在Rt△OPQ′中,根据勾股定理可计算出PQ′=
,则EQ′=PE+PQ′=
,
然后在Rt△OQ′E中,用勾股定理计算出OE=2
,由于点Q在点Q′时,OQ最短;点Q在点E时,OQ最长,于是可得OQ的长的取值范围.
(2作OQ′⊥DE于Q′,连接OE,如图2,先利用面积法计算出OQ′=
| 12 |
| 5 |
| 9 |
| 5 |
| 34 |
| 5 |
然后在Rt△OQ′E中,用勾股定理计算出OE=2
| 13 |
解答:解: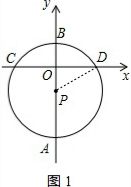 (1)连接PD,设⊙P的半径为r,
(1)连接PD,设⊙P的半径为r,
∵A(0,-8)、C(-4,0)、D(4,0),
∴OC=OD=4,OA=8,
在Rt△ODP中,OP=OA-PA=8-r,PD=r,OD=4,
∵OP2+OD2=PD2,
∴(8-r)2+42=r2,解得r=4,
即⊙P的半径为5;
(2)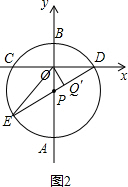 作OQ′⊥DE于Q′,连接OE,如图2,
作OQ′⊥DE于Q′,连接OE,如图2,
∵PD=5,
∴PE=5,OP=3,
∵
OQ′•PD=
•OP•OD,
∴OQ′=
=
,
在Rt△OPQ′中,PQ′=
=
,
∴EQ′=PE+PQ′=5+
=
,
在Rt△OQ′E中,OE=
=2
,
∵点Q在点Q′时,OQ最短;点Q在点E时,OQ最长,
∴OQ的长的取值范围为
≤OQ≤2
.
 (1)连接PD,设⊙P的半径为r,
(1)连接PD,设⊙P的半径为r,∵A(0,-8)、C(-4,0)、D(4,0),
∴OC=OD=4,OA=8,
在Rt△ODP中,OP=OA-PA=8-r,PD=r,OD=4,
∵OP2+OD2=PD2,
∴(8-r)2+42=r2,解得r=4,
即⊙P的半径为5;
(2)
 作OQ′⊥DE于Q′,连接OE,如图2,
作OQ′⊥DE于Q′,连接OE,如图2,∵PD=5,
∴PE=5,OP=3,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴OQ′=
| 3×4 |
| 5 |
| 12 |
| 5 |
在Rt△OPQ′中,PQ′=
| OP2-OQ′2 |
| 9 |
| 5 |
∴EQ′=PE+PQ′=5+
| 9 |
| 5 |
| 34 |
| 5 |
在Rt△OQ′E中,OE=
| OQ′2+EQ′2 |
| 13 |
∵点Q在点Q′时,OQ最短;点Q在点E时,OQ最长,
∴OQ的长的取值范围为
| 9 |
| 5 |
| 13 |
点评:本题考查了圆的综合题:熟练掌握垂径定理及其推理;会运用勾股定理计算线段的长;理解坐标与图形性质.

练习册系列答案
相关题目
 如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长.
如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长.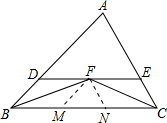 如图,∠ABC、∠ACB的平分线相交于点F.
如图,∠ABC、∠ACB的平分线相交于点F.
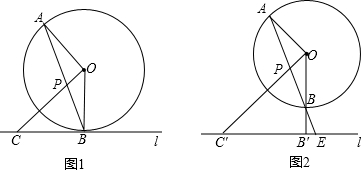
 如图所示,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9cm,AN=2cm,求△ABC的周长.
如图所示,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9cm,AN=2cm,求△ABC的周长.