题目内容
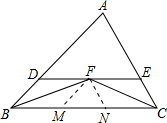 如图,∠ABC、∠ACB的平分线相交于点F.
如图,∠ABC、∠ACB的平分线相交于点F.(1)过点F作DE∥BC,分别交AB、AC于点D、E,求证:BD+EC=DE;
(2)过点F作FM∥AB交BC于点M,过点F作FN∥AC交BC于点N,求证:△FMN的周长等于BC.
考点:全等三角形的判定与性质,平行线的性质
专题:
分析:(1)根据BF和CF分别平分∠ABC和∠ACB,和DE∥BC,利用两直线平行,内错角相等和等量代换,求证出DB=DF,FE=EC.然后即可得出答案;
(2)根据DE∥BC,FM∥AB,FN∥AC,可证明四边形BDFM和四边形CEFN是平行四边形,再转化得出△FMN的周长等于BC.
(2)根据DE∥BC,FM∥AB,FN∥AC,可证明四边形BDFM和四边形CEFN是平行四边形,再转化得出△FMN的周长等于BC.
解答: 解:(1)∵在△ABC中,FB和FC分别平分∠ABC和∠ACB,
解:(1)∵在△ABC中,FB和FC分别平分∠ABC和∠ACB,
∴∠1=∠2,∠4=∠5,
∵DE∥BC,
∴∠2=∠3=∠1,∠6=∠4=∠5,
∴DB=DF,FE=EC,
∵DE=DF+FE,
∴DE=BD+EC;
(2)∵DE∥BC,FM∥AB,FN∥AC
∴四边形BDFM和四边形CEFN是平行四边形,
∴FM=BD,FN=CE,DF=BM,EF=CN,
∵BD=DF,CE=EF,
∴C△FMN=FM+FN+MN=BM+CN+MN=BC.
 解:(1)∵在△ABC中,FB和FC分别平分∠ABC和∠ACB,
解:(1)∵在△ABC中,FB和FC分别平分∠ABC和∠ACB,∴∠1=∠2,∠4=∠5,
∵DE∥BC,
∴∠2=∠3=∠1,∠6=∠4=∠5,
∴DB=DF,FE=EC,
∵DE=DF+FE,
∴DE=BD+EC;
(2)∵DE∥BC,FM∥AB,FN∥AC
∴四边形BDFM和四边形CEFN是平行四边形,
∴FM=BD,FN=CE,DF=BM,EF=CN,
∵BD=DF,CE=EF,
∴C△FMN=FM+FN+MN=BM+CN+MN=BC.
点评:本题主要考查全等三角形的判定和性质,以及对等腰三角形的判定与性质平行线段性质的理解和掌握,此题关键是求证DB=DF,FE=EC,难度不大,是一道基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
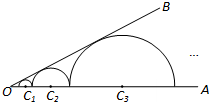 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则
如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则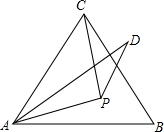 已知:如图,P为等边三角形内一点,PA=PC,AD=AC,∠PAD=∠PAB,求证:∠PDA=∠30°.
已知:如图,P为等边三角形内一点,PA=PC,AD=AC,∠PAD=∠PAB,求证:∠PDA=∠30°.
 ⊥AB于点F,DE交AC于点G.
⊥AB于点F,DE交AC于点G.