题目内容
在如图所示的正方形网格中,每个小正方形的边长为1个单位,点A的坐标为(3,0),⊙A被y轴截得的弦长BC=8.解答下列问题:
(1)求⊙A的半径;
(2)请在图中将⊙A先向上平移6个单位,再向左平移8个单位得到⊙D,并写出圆心D的坐标;
(3)过点B作⊙A的切线,交x轴负半轴于点E,求点E的坐标.

(1)求⊙A的半径;
(2)请在图中将⊙A先向上平移6个单位,再向左平移8个单位得到⊙D,并写出圆心D的坐标;
(3)过点B作⊙A的切线,交x轴负半轴于点E,求点E的坐标.

考点:圆的综合题
专题:综合题
分析:(1)根据垂径定理,由OA⊥BC得到OB=
BC=4,然后在Rt△AOB中利用勾股可计算出AB=5,即⊙A的半径为5;
(2)如图,圆平移的过程中半径不变,根据点平移的坐标变化规律,写出点A(3,0)平移后对应点D的坐标为(11,6),再画出⊙D;
(3)根据切线的性质,由BE切⊙A于B得到AB⊥BE,再证明Rt△AOB∽Rt△ABE,利用相似比可计算出AE=
,则OE=AE-OA=
,然后写出E点坐标.
| 1 |
| 2 |
(2)如图,圆平移的过程中半径不变,根据点平移的坐标变化规律,写出点A(3,0)平移后对应点D的坐标为(11,6),再画出⊙D;
(3)根据切线的性质,由BE切⊙A于B得到AB⊥BE,再证明Rt△AOB∽Rt△ABE,利用相似比可计算出AE=
| 25 |
| 3 |
| 16 |
| 3 |
解答:解:(1)∵OA⊥BC,
∴OC=OB=
BC=
×8=4,
∵A(3,0),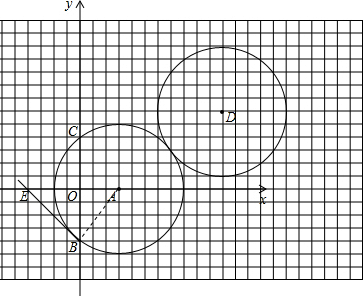
∴OA=3,
在Rt△AOB中,∵OA=3,OB=4,
∴AB=
=5,
即⊙A的半径为5;
(2)如图,D点坐标为(11,6);
(3)∵BE切⊙A于B,
∴AB⊥BE,
∴∠ABE=90°,
∵∠OAB=∠BAE,
∴Rt△AOB∽Rt△ABE,
∴
=
,即
=
,
∴AE=
,
∴OE=AE-OA=
,
∴E点坐标为(-
,0).
∴OC=OB=
| 1 |
| 2 |
| 1 |
| 2 |
∵A(3,0),

∴OA=3,
在Rt△AOB中,∵OA=3,OB=4,
∴AB=
| OA2+OB2 |
即⊙A的半径为5;
(2)如图,D点坐标为(11,6);
(3)∵BE切⊙A于B,
∴AB⊥BE,
∴∠ABE=90°,
∵∠OAB=∠BAE,
∴Rt△AOB∽Rt△ABE,
∴
| AO |
| AB |
| AB |
| AE |
| 3 |
| 5 |
| 5 |
| AE |
∴AE=
| 25 |
| 3 |
∴OE=AE-OA=
| 16 |
| 3 |
∴E点坐标为(-
| 16 |
| 3 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、切线的性质;会利用勾股定理和相似比计算线段的长;了解坐标平面内点平移后的坐标变化规律;理解坐标与图形的性质.

练习册系列答案
相关题目
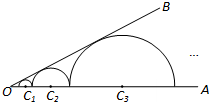 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则
如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则
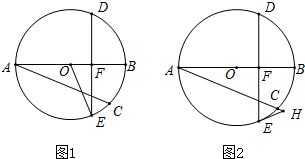 ⊥AB于点F,DE交AC于点G.
⊥AB于点F,DE交AC于点G. 如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.
如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.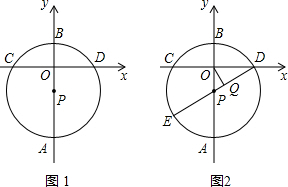
 如图,在⊙O中,∠AOB=60°,AB=3cm,则劣弧AB的长为
如图,在⊙O中,∠AOB=60°,AB=3cm,则劣弧AB的长为