题目内容
某公司对一种新型产品的产销情况进行了营销调查,发现年产量为x(吨)时,所需的费用y(万元)与(x2+60x+800)成正比例,投入市场后当年能全部售出且发现每吨的售价p(单位:万元)由基础价与浮动价两部分组成,其中基础价是固定不变的,浮动价与x成正比例,比例系数为-
.在营销中发现年产量为20吨时,所需的全部费用是240万元,并且年销售量W最大值为55万元.(注:年利润=年销售额-全部费用)
(1)求y(万元)与x(吨)之间满足的函数关系式;
(2)求年销售利润W与年产量x(吨)之间满足的函数关系式;
(3)当年销售利润最大时,每吨的售价是多少万元?
| 1 |
| 20 |
(1)求y(万元)与x(吨)之间满足的函数关系式;
(2)求年销售利润W与年产量x(吨)之间满足的函数关系式;
(3)当年销售利润最大时,每吨的售价是多少万元?
考点:二次函数的应用
专题:
分析:(1)设y=k(x2+60x+800),由待定系数法建立方程求出k值即可;
(2)设基础价为a,则p=a-
x,根据年利润=年销售额-全部费用就可以表示出W与x的关系式;
(3)根据(2)的结论把a、x的值代入p=a-
x,求出p即可.
(2)设基础价为a,则p=a-
| 1 |
| 20 |
(3)根据(2)的结论把a、x的值代入p=a-
| 1 |
| 20 |
解答:(1)设y=k(x2+60x+800),由题意,得
240=k(202+60×20+800),
解得:k=
,
∴y=
x2+6x+80;
(2)设基础价为a,则p=a-
x,
∴W=px-y=(a-
x)x-(
x2+6x+80)=-
[x-
×10(a-6)]2+
×5(a-6)2-80.
∵W最大值为55万元,
∴
×5(a-6)2-80=55,
解得:a1=15,a2=-3(舍去),
∴W=-
[x-
10(15-6)]2+
×5(15-6)2-80=-
(x-30)2+55;
(3)∵W=-
(x-30)2+55,
∴当x=30(吨)时,年销售利润最大,
∴p=a-
x=15-
×30=13.5(万元/吨),
∴当年销售利润最大时,每吨的售价是13.5万元.
240=k(202+60×20+800),
解得:k=
| 1 |
| 10 |
∴y=
| 1 |
| 10 |
(2)设基础价为a,则p=a-
| 1 |
| 20 |
∴W=px-y=(a-
| 1 |
| 20 |
| 1 |
| 10 |
| 3 |
| 20 |
| 1 |
| 3 |
| 1 |
| 3 |
∵W最大值为55万元,
∴
| 1 |
| 3 |
解得:a1=15,a2=-3(舍去),
∴W=-
| 3 |
| 20 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 20 |
(3)∵W=-
| 3 |
| 20 |
∴当x=30(吨)时,年销售利润最大,
∴p=a-
| 1 |
| 20 |
| 1 |
| 20 |
∴当年销售利润最大时,每吨的售价是13.5万元.
点评:本题考查了销售问题的年利润=年销售额-全部费用的关系式的运用,二次函数的解析式的运用,二次函数的最值的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
若x<y成立,则下列不等式成立的是( )
| A、-3x<-3y |
| B、x-2<y-2 |
| C、-(x-2)<-(y-2) |
| D、-x+2<-y+2 |
 小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)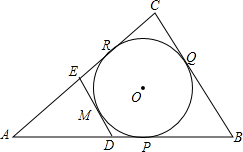 如图,⊙O内切于△ABC,P,Q,R为切点,⊙O的切线DE∥BC,M为切点,D,E分别在AB,AC上,已知BC=2,△ABC的周长为8,⊙O的半径为1,则S△ADE=
如图,⊙O内切于△ABC,P,Q,R为切点,⊙O的切线DE∥BC,M为切点,D,E分别在AB,AC上,已知BC=2,△ABC的周长为8,⊙O的半径为1,则S△ADE= 如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.
如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.