题目内容
 如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.
如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,DE=3,AF=8.(1)求AC的长;
(2)求
| CD2 |
| BC2 |
考点:相似三角形的判定与性质
专题:
分析:(1)易证△ADC∽△AEF,由相似三角形的性质:对应边的比值相等即可求出AC的长;
(2)首先利用相似三角形的性质可得到CD:BC的值,进而可求出
的值.
(2)首先利用相似三角形的性质可得到CD:BC的值,进而可求出
| CD2 |
| BC2 |
解答:解:(1)∵EF∥DC,
∴△ADC∽△AEF,
∴AC:AD=AF:AE,
∵AE=6,DE=3,
∴AD=9,
∵AF=8,
∴AC:9=8:6,
∴AC=12,
(2)∵EF∥DC,
∴∠AFE=∠B,
∵∠AFE=∠B,
∴∠ACD=∠B,
又∵∠A=∠A,
∴△ACD∽△ABC,
∴CD:BC=AC:AB,
∵EF∥DC,
∴AFE∽△ABC,
∴AC:AB=AE:AF
∴CD:BC=AE:AF=6:8=3:4,
∴
=(
)2=
.
∴△ADC∽△AEF,

∴AC:AD=AF:AE,
∵AE=6,DE=3,
∴AD=9,
∵AF=8,
∴AC:9=8:6,
∴AC=12,
(2)∵EF∥DC,
∴∠AFE=∠B,
∵∠AFE=∠B,
∴∠ACD=∠B,
又∵∠A=∠A,
∴△ACD∽△ABC,
∴CD:BC=AC:AB,
∵EF∥DC,
∴AFE∽△ABC,
∴AC:AB=AE:AF
∴CD:BC=AE:AF=6:8=3:4,
∴
| CD2 |
| BC2 |
| 3 |
| 4 |
| 9 |
| 16 |
点评:本题考查了相似三角形的判定和性质,解题的关键是注意相等比例式的替换,题目的综合性较强,难度不小.

练习册系列答案
相关题目
 在某山区需要修建一条高速公路,在施工过程中要沿直线AB打通一条隧道,动工前,应先测隧道BC的长,现测得∠ABD=150°,∠D=60°,BD=10km,CD=5km,请根据上述数据,求出隧道BC的长.
在某山区需要修建一条高速公路,在施工过程中要沿直线AB打通一条隧道,动工前,应先测隧道BC的长,现测得∠ABD=150°,∠D=60°,BD=10km,CD=5km,请根据上述数据,求出隧道BC的长.将直线y=-3x+1向下平移2个单位得到直线l,则直线l的解析式为( )
| A、y=-3x+2 |
| B、y=-3x-2 |
| C、y=-3x-1 |
| D、y=-3x+3 |
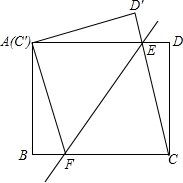 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,BC于点F,连接AF、CE.
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,BC于点F,连接AF、CE.
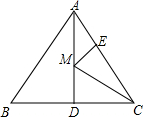 如图,等边△ABC的边长为6,面积为9
如图,等边△ABC的边长为6,面积为9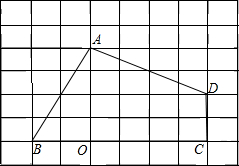 如图,在8×6正方形网格图中,每个小正方形边长均为1,点O和四边形ABCD的顶点均在小正方形的顶点上.
如图,在8×6正方形网格图中,每个小正方形边长均为1,点O和四边形ABCD的顶点均在小正方形的顶点上.