题目内容
已知关于x的一元二次方程为(2a-1)x2-(4a+2)x+2a+3=0
(1)求出方程的根;
(2)当a为何整数时,此方程的两个根都为正整数?
(1)求出方程的根;
(2)当a为何整数时,此方程的两个根都为正整数?
考点:根的判别式,解一元二次方程-因式分解法
专题:计算题
分析:(1)先计算判别式的值,然后根据求根公式解方程即可;
(2)由于一个根为2,只要x1=
为正整数即可,而x1=1+
,利用整数的整除性得到2a-1=1,2,4时,方程的两个根都为正整数,然后确定整数a的值.
(2)由于一个根为2,只要x1=
| 2a+3 |
| 2a-1 |
| 4 |
| 2a-1 |
解答:解:(1)△=(4a+2)2-4(2a-1)(2a+3)
=16,
x=
,
所以x1=
,x2=2;
(2)x1=
=1+
,
当2a-1=1,2,4时,方程的两个根都为正整数,
所以整数a为1.
=16,
x=
4a+2±
| ||
| 2(2a-1) |
所以x1=
| 2a+3 |
| 2a-1 |
(2)x1=
| 2a+3 |
| 2a-1 |
| 4 |
| 2a-1 |
当2a-1=1,2,4时,方程的两个根都为正整数,
所以整数a为1.
点评:本题考查了利用一元二次方程根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
 如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是( )
如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是( )| A、|b|>|a| |
| B、a-b<0 |
| C、a+b<0 |
| D、ab<0 |
已知等腰三角形的周长为16,若设腰长为x,则x的取值范围是( )
| A、4≤x≤8 | ||
| B、4<x<8 | ||
C、
| ||
D、
|
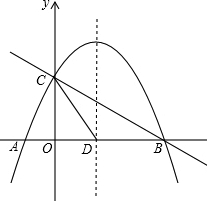 如图,抛物线y=-
如图,抛物线y=- 在某山区需要修建一条高速公路,在施工过程中要沿直线AB打通一条隧道,动工前,应先测隧道BC的长,现测得∠ABD=150°,∠D=60°,BD=10km,CD=5km,请根据上述数据,求出隧道BC的长.
在某山区需要修建一条高速公路,在施工过程中要沿直线AB打通一条隧道,动工前,应先测隧道BC的长,现测得∠ABD=150°,∠D=60°,BD=10km,CD=5km,请根据上述数据,求出隧道BC的长.