Question

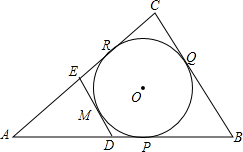如图，⊙O内切于△ABC，P，Q，R为切点，⊙O的切线DE∥BC，M为切点，D，E分别在AB，AC上，已知BC=2，△ABC的周长为8，⊙O的半径为1，则S_△ADE=

 

．

Answer 1

考点：三角形的内切圆与内心

专题：计算题

分析：连结OM、OQ，如图，根据切线的性质得OM⊥DE，OQ⊥BC，而DE∥BC，利用平行线的性质得到点M、O、Q共线，即MQ=2，再利用切线长定理得CR=CQ，BP=BQ，EM=ER，DM=DP，则CR+BP=BC=2，由于AC+AB+BC=8，可计算出AE+EM+AD+DM=4，即△ADE的周长为4，接着证明△ADE∽△ABC，利用相似的性质得到

DE

BC

=

△ADE的周长

△ABC的周长

，则可计算出DE=

1

2

BC=1，则可计算出S_梯形BDEC=3，然后利用相似的性质得到

S△ADE

S△ABC

=（

DE

BC

）²=

1

4

，即

S△ADE

S△ADE+3

=

1

4

，利用比例性质可计算得S_△ADE=1．

解答：解：连结OM、OQ，如图，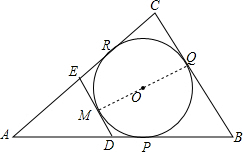
∵点M和点Q为切点，
∴OM⊥DE，OQ⊥BC，
∵DE∥BC，
∴OQ⊥DE，
∴点M、O、Q共线，即MQ=2，
∵P，Q，R、M为切点，
∴CR=CQ，BP=BQ，EM=ER，DM=DP，
∴CR+BP=BC=2，
∵AC+AB+BC=8，
∴AR+AP=8-2-2=4，
∴AE+EM+AD+DM=4，
∴△ADE的周长为4，
∵DE∥BC，
∴△ADE∽△ABC，
∴

DE

BC

=

△ADE的周长

△ABC的周长

=

4

8

，
∴DE=

1

2

BC=1，
∴S_梯形BDEC=

1

2

（1+2）•2=3，
∵△ADE∽△ABC，
∴

S△ADE

S△ABC

=（

DE

BC

）²=

1

4

，
∴

S△ADE

S△ADE+3

=

1

4

，
∴S_△ADE=1．
故答案为1．

点评：本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了相似三角形的判定与性质．