题目内容
有甲、乙、丙三个三角形,已知三个三角形的内角度数如图(1)、(2)、(3)所示,

(1)请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.
(2)利用第(1)小题的分割方法,求将一个等腰三角形分割成两个等腰三角形,原等腰三角形的顶角度数?(直接写出答案即可)

(1)请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.
(2)利用第(1)小题的分割方法,求将一个等腰三角形分割成两个等腰三角形,原等腰三角形的顶角度数?(直接写出答案即可)
考点:作图—复杂作图,等腰三角形的性质
专题:
分析:(1)图1中只要找到斜边中点,然后连接直角顶点和斜边中点,那么分成的两个三角形就是等腰三角形;图2,图3要先根据三角形的内角和求出另一角的度数,然后看看是否能分成等腰三角形.
(2)本题要利用三角形内角和定理求解.由于本题中经过等腰三角形顶点的直线没有明确是经过顶角的顶点还是底角的顶点,因此本题要分情况讨论.
(2)本题要利用三角形内角和定理求解.由于本题中经过等腰三角形顶点的直线没有明确是经过顶角的顶点还是底角的顶点,因此本题要分情况讨论.
解答:解:(1)如图所示:

(2)设该等腰三角形的底角是x;
①当过顶角的顶点的直线把它分成了两个等腰三角形,如图①,则AC=BC,AD=CD=BD,
设∠A=x°,
则∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°,
∴x+x+x+x=180,
解得x=45,
则顶角是90°;
②如图②,AC=BC=BD,AD=CD,
设∠B=x°,
∵AC=BC,
∴∠A=∠B=x°,
∵AD=CD,
∴∠ACD=∠A=x°,
∴∠BDC=∠A+∠ACD=2x°,
∵BC=BD,
∴∠BCD=∠BDC=2x°,
∴∠ACB=3x°,
∴x+x+3x=180,x=36°,则顶角是108°.
③当过底角的角平分线把它分成了两个等腰三角形,如图③,则有AC=BC,AB=AD=CD,
设∠C=x°,
∵AD=CD,
∴∠CAD=∠C=x°,
∴∠ADB=∠CAD+∠C=2x°,
∵AD=AB,
∴∠B=∠ADB=2x°,
∵AC=BC,
∴∠CAB=∠B=2x°,
∵∠CAB+∠B+∠C=180°,
∴x+2x+2x=180,
x=36°,
则顶角是36°.
④当∠A=x°,∠ABC=∠ACB=3x°时,也符合,如图④
AD=BD,BC=DC,
∠A=∠ABD=x,∠DBC=∠BDC=2x,
则x+3x+3x=180°,
x=
综上可知:顶角度数:90°;36°;108°;
.

(2)设该等腰三角形的底角是x;
①当过顶角的顶点的直线把它分成了两个等腰三角形,如图①,则AC=BC,AD=CD=BD,
设∠A=x°,
则∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°,
∴x+x+x+x=180,

解得x=45,
则顶角是90°;
②如图②,AC=BC=BD,AD=CD,
设∠B=x°,
∵AC=BC,
∴∠A=∠B=x°,
∵AD=CD,
∴∠ACD=∠A=x°,
∴∠BDC=∠A+∠ACD=2x°,
∵BC=BD,
∴∠BCD=∠BDC=2x°,
∴∠ACB=3x°,
∴x+x+3x=180,x=36°,则顶角是108°.
③当过底角的角平分线把它分成了两个等腰三角形,如图③,则有AC=BC,AB=AD=CD,
设∠C=x°,
∵AD=CD,
∴∠CAD=∠C=x°,
∴∠ADB=∠CAD+∠C=2x°,
∵AD=AB,
∴∠B=∠ADB=2x°,
∵AC=BC,

∴∠CAB=∠B=2x°,
∵∠CAB+∠B+∠C=180°,
∴x+2x+2x=180,
x=36°,
则顶角是36°.
④当∠A=x°,∠ABC=∠ACB=3x°时,也符合,如图④
AD=BD,BC=DC,
∠A=∠ABD=x,∠DBC=∠BDC=2x,
则x+3x+3x=180°,
x=
| 180° |
| 7 |
综上可知:顶角度数:90°;36°;108°;
| 180° |
| 7 |
点评:本题考查了等腰三角形的性质及其判定.作此题的时候,首先大致画出符合条件的图形,然后根据等腰三角形的性质、三角形的内角和定理及其推论找到角之间的关系,列方程求解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图,已知正方形ABCD,以CD为边作等边△DEC,并连接AE、BC,求S△EMN:S△ADN.
如图,已知正方形ABCD,以CD为边作等边△DEC,并连接AE、BC,求S△EMN:S△ADN. 如图,在8×6正方形网格图中,每个小正方形边长均为1,点O和四边形ABCD的顶点均在小正方形的顶点上.
如图,在8×6正方形网格图中,每个小正方形边长均为1,点O和四边形ABCD的顶点均在小正方形的顶点上.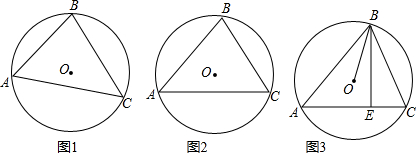
 求这个立体图形的表面积(求6个面).
求这个立体图形的表面积(求6个面). 如图,已知∠AOB=∠COD=90°,OC平分∠AOB,OE是∠BOD的三等分线,求∠COE的度数.
如图,已知∠AOB=∠COD=90°,OC平分∠AOB,OE是∠BOD的三等分线,求∠COE的度数.