题目内容
如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,用n表示这个规律的代数式为 .


考点:规律型:图形的变化类
专题:
分析:第一个图形有1个小石子,第二个图形有5=2+3个小石子,第三个图形有12=3+4+5个小石子,…第n个图形有n+n+1+n+2+n+3+••[n+(n-1)]=n2+
个小石子,由此得出答案解决问题.
| n(n-1) |
| 2 |
解答:解:第一个图形有1个,
第二个图形有5=2+3个,
第三个图形有12=3+4+5个,
…
第n个图形有n+n+1+n+2+n+3+••[n+(n-1)]=n2+
个.
故答案为:n2+
.
第二个图形有5=2+3个,
第三个图形有12=3+4+5个,
…
第n个图形有n+n+1+n+2+n+3+••[n+(n-1)]=n2+
| n(n-1) |
| 2 |
故答案为:n2+
| n(n-1) |
| 2 |
点评:此题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
 已知△ABC中,AB=17,BC=21,CA=10,求BC边上的高AD.
已知△ABC中,AB=17,BC=21,CA=10,求BC边上的高AD.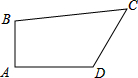 四边形ABCD,∠A=90°.AB=2,AD=2
四边形ABCD,∠A=90°.AB=2,AD=2 在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过点B作BE⊥CD的延长线于E,连接AE,过点A作AF⊥AE交CD于点F.
在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过点B作BE⊥CD的延长线于E,连接AE,过点A作AF⊥AE交CD于点F. 用长14m的篱笆围成如图所示的鸡舍,门MN宽2m,怎样设计才能使鸡舍的面积最大?
用长14m的篱笆围成如图所示的鸡舍,门MN宽2m,怎样设计才能使鸡舍的面积最大?