题目内容
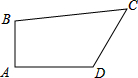 四边形ABCD,∠A=90°.AB=2,AD=2
四边形ABCD,∠A=90°.AB=2,AD=2| 3 |
考点:勾股定理的逆定理,特殊角的三角函数值
专题:
分析:连结BD,先根据勾股定理求出BD的长度,由正弦函数的定义得到∠ADB=30°,再根据勾股定理的逆定理判断出△BCD是直角三角形,得出∠BDC=90°,然后根据∠ADC=∠ADB+∠BDC求解即可.
解答: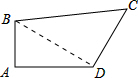 解:如图,连结BD.
解:如图,连结BD.
∵∠A=90°,AB=2,AD=2
,
∴BD=
=4.
∵sin∠ADB=
=
=
,
∴∠ADB=30°.
在△BCD中,∵BD2+CD2=42+32=52=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=30°+90°=120°.
 解:如图,连结BD.
解:如图,连结BD.∵∠A=90°,AB=2,AD=2
| 3 |
∴BD=
| AB2+AD2 |
∵sin∠ADB=
| AB |
| BD |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠ADB=30°.
在△BCD中,∵BD2+CD2=42+32=52=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=30°+90°=120°.
点评:本题考查的是勾股定理及其逆定理,能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.

练习册系列答案
相关题目
 如图,要建一个苗圃,它的宽是a=4.8厘米,高b=3.6米.苗圃总长是10米.
如图,要建一个苗圃,它的宽是a=4.8厘米,高b=3.6米.苗圃总长是10米.

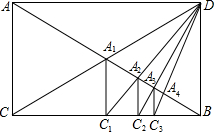 如图,对于任意线段AB,可以构造以AB为对角线的矩形ACBD.连接CD,与AB交于A1点,过A1作BC的垂线段A1C1,垂足为C1;连接C1D,与AB交于A2点,过A2作BC的垂线段A2C2,垂足为C2;连接C2D,与AB交于A3点,过A3作BC的垂线段A3C3,垂足为C3…如此下去,可以依次得到点A4,A5,…,An.如果设AB的长为1,依次可求得A1B,A2B,A3B…的长,则AnB的长为(用n的代数式表示)( )
如图,对于任意线段AB,可以构造以AB为对角线的矩形ACBD.连接CD,与AB交于A1点,过A1作BC的垂线段A1C1,垂足为C1;连接C1D,与AB交于A2点,过A2作BC的垂线段A2C2,垂足为C2;连接C2D,与AB交于A3点,过A3作BC的垂线段A3C3,垂足为C3…如此下去,可以依次得到点A4,A5,…,An.如果设AB的长为1,依次可求得A1B,A2B,A3B…的长,则AnB的长为(用n的代数式表示)( )