Question

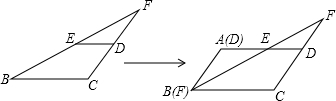
在△ABC中，∠BAC=90°，AB=AC，点D是AB的中点，连接CD，过点B作BE⊥CD的延长线于E，连接AE，过点A作AF⊥AE交CD于点F．
（1）若AE=5，求EF；
（2）求证：CD=2BE+DE．

Answer 1

考点：全等三角形的判定与性质,等腰直角三角形

专题：

分析：（1）证出B、E、A、C四点共圆，推出∠AEF=∠ABC=45°，求出∠AFE=45°=∠AEF，推出AE=AF即可；
（2）过A作AM⊥EF于M，求出AM=MF，AD=BD，∠BED=∠AMD=90°，证△AMD≌△BED（AAS），推出BE=AM=MF，DE=DM，证△EAB≌△FAC，推出BE=CF，即可得出答案．

解答：（1）解：∵在△ABC中，∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∵BE⊥CD，
∴∠BEC=∠BAC=90°，
∴B、E、A、C四点共圆，
∴∠ABE=∠ACF，∠AEF=∠ABC=45°，
∵AE⊥AF，
∴∠EAF=90°，
∴∠AFE=45°=∠AEF，
∴AE=AF，
∵AE=5，
∴AF=5，
由勾股定理得：EF=

52+52

=5

2

；

（2）证明：过A作AM⊥EF于M，
∵∠EAF=90°，AE=AF，
∴∠MAF=

1

2

∠EAF=45°=∠AFM，
∴AM=MF，
∵D为AB中点，
∴AD=BD，
∵BE⊥CD，AM⊥CD，
∴∠BED=∠AMD=90°，
在△AMD和△BED中，

∠AMD=∠BED ∠ADM=∠BDE AD=BD

∴△AMD≌△BED（AAS），
∴BE=AM=MF，DE=DM，
∵∠EAF=∠CAD=90°，
∴∠EAB=∠FAC=90°-∠DAF，
在△EAB和△FAC中，

AE=AF ∠EAB=∠FAC AB=AC

∴△EAB≌△FAC（SAS），
∴BE=CF，
∴CD=CF+MF+DM=2BE+DE．

点评：本题考查了全等三角形的性质和判定，圆内接四边形的条件，等腰三角形的性质和判定的应用，主要考查学生综合运用定理进行推理的能力．