题目内容
6.一束光线从y轴上的点A(0,m)出发,经过x轴上的点M$({\frac{3}{4},0})$反射后恰好经过点B(3,3),则m=1.分析 过B点作X轴的垂线与X轴相交于点D,由已知条件可以得到△OAC∽△DBC,从而得到OC和OA,CD,BD的数量关系,求出OA的长,进而求出m的值.
解答 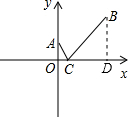 解:过B点作X轴的垂线与X轴相交于点D,则BD⊥CD,
解:过B点作X轴的垂线与X轴相交于点D,则BD⊥CD,
∵A点经过点C反射后经过B点,
∴∠OCA=∠DCB,
∴△OAC∽△DBC,
∴$\frac{OA}{BD}=\frac{OC}{CD}$,
∴$\frac{m}{3}=\frac{\frac{3}{4}}{\frac{9}{4}}$,
∴m=1,
故答案为1.
点评 本题考查镜面反射的原理与性质、三角形相似的判定和性质,构造相似三角形是解决本题关键.

练习册系列答案
相关题目
16.由4名同学每人写一个实系数一元二次方程,所得的四个方程中恰有两个无实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{8}$ |
14.若关于x的不等式组$\left\{\begin{array}{l}{x-m<0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个,则关于x的一元二次方程8x2-8x+m=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有一个实数根 |
 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.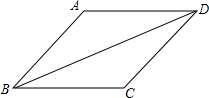 如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.
如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.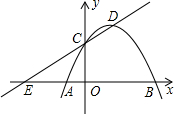 如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.