题目内容
3.如图1,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$的图象交于A(m,6),B(-3,n)两点.(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)如图2,延长BO交反比例函数y=$\frac{6}{x}$的图象于点C,连结AC,则△ABC的面积是16(直接写出答案)
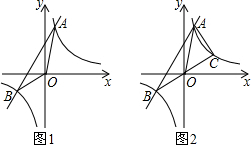
分析 (1)把A与B坐标代入反比例解析式求出m与n的值,确定出A与B坐标,代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)根据直线解析式求得与y轴的交点,然后根据三角形的面积公式即可求得;
(3)易得△AOB和△AOC是等底同高,即可求得△ABC的面积.
解答 解:(1)把A(m,6),B(-3,n)代入反比例函数y=$\frac{6}{x}$,得:m=1,n=-2,即A(1,6),B(-3,-2),
把A与B坐标代入一次函数解析式得:$\left\{\begin{array}{l}{k+b=6}\\{-3k+b=-2}\end{array}\right.$,
解得:k=2,b=4,
则一次函数解析式为y=2x+4;
(2)由一次函数解析式为y=2x+4可知,直线与y轴的交点为(0,4),
∴S△AOB=$\frac{1}{2}$×4×(1+3)=8;
(3)由图象可知B、C关于O点对称,
∴OB=OC,
∴△AOB和△AOC是等底同高,
∴S△ABC=2S△AOB=16.
故答案为16.
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法求一次函数解析式,三角形的面积等,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
13.一个圆锥的主视图是边长为4的等边三角形,这个这个圆锥的侧面积为( )
| A. | (4$\sqrt{3}$+4)π | B. | (8$\sqrt{3}$+4)π | C. | 12π | D. | 8π |
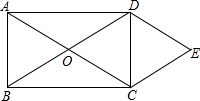 如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.
如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.
 如图,在正方形ABCD中,BD为一条对角线,点P为CD边上一点,A连接AP,并将△ADP平移使AD与BC边重合,P点落在DC的延长线上的一点G处,过G点作GH⊥BD于点H,连接HP和HC
如图,在正方形ABCD中,BD为一条对角线,点P为CD边上一点,A连接AP,并将△ADP平移使AD与BC边重合,P点落在DC的延长线上的一点G处,过G点作GH⊥BD于点H,连接HP和HC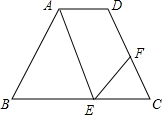 如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°