题目内容
13.菱形OABC的边长为5,顶点C的坐标为(a,4),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B.(1)求点C的坐标;
(2)求k的值.
分析 (1)首先根据题意画出图形,然后过点C作CD⊥x轴于点D,由菱形OABC的边长为5,顶点C的坐标为(a,4),可求得a的值,继而求得点C的坐标;
(2)由菱形OABC的边长为5,可求得点B的坐标,又由反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,即可求得k的值.
解答 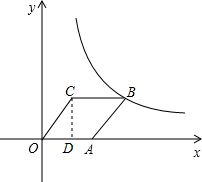 解:(1)如图,过点C作CD⊥x轴于点D,
解:(1)如图,过点C作CD⊥x轴于点D,
∵菱形OABC的边长为5,顶点C的坐标为(a,4),
∴OC=5,CD=4,
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=3,
∴点C的坐标为:(3,4);
(2)∵菱形OABC的边长为5,点C的坐标为:(3,4);
∴点B的坐标为:(8,4);
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,
∴k=xy=8×4=32.
点评 此题考查了菱形的性质、待定系数法求反比例函数的解析式以及勾股定理.注意根据菱形的性质求得点C与点B的坐标是关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
4.关于x的一元二次方程$\frac{1}{2}{x}^{2}$+3x+k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k$<\frac{9}{2}$ | B. | k=$\frac{9}{4}$ | C. | k$≥\frac{9}{2}$ | D. | k$>\frac{9}{4}$ |
9.已知关于x的方程x4-ax2+1=0无实数根,则实数a的取值范围为( )
| A. | -2<a<2 | B. | a<0 | C. | -2<a<0 | D. | a<2 |



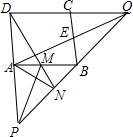 如图,在正方形ABcD中,M为AB中点,连结DM并延长DM到N,使NA2=NM•ND.
如图,在正方形ABcD中,M为AB中点,连结DM并延长DM到N,使NA2=NM•ND.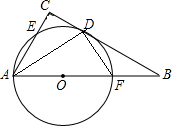 如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证:
如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证: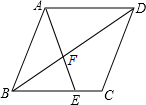 如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.
如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.