题目内容
17.已知直线y=kx+b与y=3x平行,与y=$\frac{1}{2}$x+2交于y轴上一点,则k=3,b=2,直线的解析式是y=3x+2.分析 先利用两直线平行得到k=3,再求出直线y=$\frac{1}{2}$x+2与y轴的交点坐标,然后那此交点坐标代入y=3x+b中求出b即可得到直线解析式.
解答 解:∵直线y=kx+b与y=3x平行,
∴k=3,
∵当x=0时,y=$\frac{1}{2}$x+2=2,
∴直线y=$\frac{1}{2}$x+2与y轴的交点坐标为(0,2),
把(0,2)代入y=3x+b得b=2,
∴直线解析式为y=3x+2.
故答案为3,2,y=3x+2.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
7.已知:点A(a,b),B(a+1,b-2)均在正比例函数y=kx(k≠0)的图象上,则k值为( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |

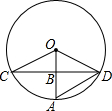 如图,在⊙O中,已知CD是垂直平分半径OA的弦.
如图,在⊙O中,已知CD是垂直平分半径OA的弦. 如图,在平行四边形ABCD中,E在AB上,CE,BD交于F,若AE:DE=4:3,则S△CBF:S△DCF=7:3.
如图,在平行四边形ABCD中,E在AB上,CE,BD交于F,若AE:DE=4:3,则S△CBF:S△DCF=7:3.