题目内容
7.图1、图2分别是10×10的正方形网格,网格中的每个小正方形的边长都是1,线段AB的端点都在小正方形的顶点上.请在图1、图2中各画一个图形,分别满足下列要求: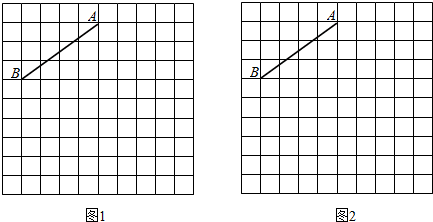
(1)在图1中,画出一个以线段AB为一边的菱形ABCD(非正方形),所画的菱形的各顶点必须在小正方形的顶点上,并且其面积是15;
(2)在图2中,画出一个以线段AB为腰的等腰梯形,所画等腰梯形的各顶点必须在小正方形的顶点上,且其周长为10+3$\sqrt{10}$.
分析 (1)根据条件一个底为5高为3的菱形即可.
(2)画一个等腰梯形,腰AB=CD=5,底分别为$\sqrt{10}$,2$\sqrt{10}$即可.
解答 解:(1)满足条件的菱形ABCD如图1所示.AB=BC=AD=CD=5,面积为15.
(2)满足条件的等腰梯形ABCD如图2所示.BC∥AD,AB=CD=5,BC=$\sqrt{10}$,AD=2$\sqrt{10}$,周长为10+3$\sqrt{10}$.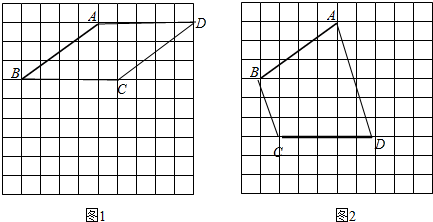
点评 本题考查作图设计由应用、菱形的性质、等腰梯形性质等知识,解题的关键是先根据数量关系确定相关线段的长度,然后画出图形,体现了数形结合的思想,是一个好题目,中考常考题型.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.在直角坐标系中,长方形ABCD的边AB可表示成(2,y)(-1≤y≤3),边BC可表示成(x,3)(2≤x≤5),则点D的坐标是( )
| A. | (5,3) | B. | (5,-1) | C. | (-1,2) | D. | (2,-1) |
15.为了解我区七年级6000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计.下列判断:
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.如表列出了皮球反弹高度和下落高度的数据,其中d表示皮球的下落高度,h表示皮球落地后的反弹高度(单位:cm)
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是函数?
(2)当下落高度是100cm时,皮球的反弹高度是多少?
(2)预测下落高度是90cm时,皮球的反弹高度是多少?
| d | 50 | 80 | 100 | 150 |
| h | 25 | 40 | 50 | 75 |
(2)当下落高度是100cm时,皮球的反弹高度是多少?
(2)预测下落高度是90cm时,皮球的反弹高度是多少?
19.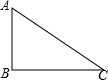 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
16. 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{6}$ | C. | 3 | D. | 4 |
 -$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$
-$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$