题目内容
6. 如图,在平行四边形ABCD中,E在AB上,CE,BD交于F,若AE:DE=4:3,则S△CBF:S△DCF=7:3.
如图,在平行四边形ABCD中,E在AB上,CE,BD交于F,若AE:DE=4:3,则S△CBF:S△DCF=7:3.
分析 根据平行四边形的性质得到AD∥BC,AD=BC,通过△DEF∽△BCF,得到$\frac{DE}{BC}=\frac{DF}{BF}$,求得$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{DE}{AD}$=$\frac{3}{7}$,于是得到结论.
解答 解:在平行四边形ABCD中,
∵AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴$\frac{DE}{BC}=\frac{DF}{BF}$,
∵AE:DE=4:3,
∴$\frac{DE}{AD}=\frac{3}{7}$,
∴$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{DE}{AD}$=$\frac{3}{7}$,
∴S△CBF:S△DCF=BF:DF=7:3,
故答案为:7:3.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,知道等高不等底的三角形的面积的比等于底的比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.某地的国际标准时间是指该地与格林尼治的时差.下表是同一时刻5个城市的国际标准时间
北京时间下午6时,纽约的当地时间为17时.
| 城市 | 多伦多 | 纽约 | 伦敦 | 北京 | 东京 |
| 国际标准时间(单位:时) | -4 | -5 | 0 | +8 | +9 |
11.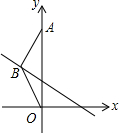 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
 如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )
如图,在△ABO中,BA=BO,OA=3,OA在y轴的正半轴上,若点B在直线y=-$\frac{1}{2}$x+1上,△ABO的面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
18.在直角坐标系中,长方形ABCD的边AB可表示成(2,y)(-1≤y≤3),边BC可表示成(x,3)(2≤x≤5),则点D的坐标是( )
| A. | (5,3) | B. | (5,-1) | C. | (-1,2) | D. | (2,-1) |
15.为了解我区七年级6000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计.下列判断:
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
①这种调查方式是抽样调查;
②6000名学生是总体;
③每名学生的数学成绩是个体;
④500名学生是总体的一个样本.
其中正确的判断有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16. 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{6}$ | C. | 3 | D. | 4 |