题目内容
5.底边长为8的等腰三角形内接于⊙O中,已知⊙O的半径为5,求等腰三角形的腰长.分析 ①当是锐角三角形时;②当该等腰三角形是钝角三角形时;由垂径定理可得出BD的长,再根据勾股定理求出OD的长,进而可得出结论.
解答 解: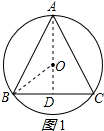 ①当等腰三角形是锐角三角形时,如图1所示:
①当等腰三角形是锐角三角形时,如图1所示:
连接AO并延长交BC于点D,连接OB,
∵AB=AC,
∴AO⊥BC,
∵BC=8,
∴BD=4,
在Rt△OBD中,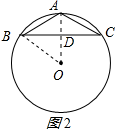
∵OB=5,BD=4,
∴OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AD=AO+OD=5+3=8,
在Rt△ABD中,
∵BD=4,AD=8,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$;
②当等腰三角形是钝角三角形时,如图2所示:
连接OA交BC于D,连接OB,
同理得:OD=3,
∴AD=OA-OD=2,
∴AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
综上所述,AB的长度是4$\sqrt{5}$或2$\sqrt{5}$.
点评 本题考查的是三角形的外接圆与外心,垂径定理,勾股定理;根据题意画出图形,利用数形结合求解是解答此题的关键,注意分类讨论.

练习册系列答案
相关题目
16.某地的国际标准时间是指该地与格林尼治的时差.下表是同一时刻5个城市的国际标准时间
北京时间下午6时,纽约的当地时间为17时.
| 城市 | 多伦多 | 纽约 | 伦敦 | 北京 | 东京 |
| 国际标准时间(单位:时) | -4 | -5 | 0 | +8 | +9 |
20.已知(a+3)2+|b-2|+2=b,则a、b的值是( )
| A. | a=-3,b为任意值 | B. | a=3,b为任意值 | C. | a=-3,b≥2 | D. | 不存在这样的a、b |
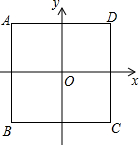 如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.