题目内容
3.一个两位数,十位数字与个位数字之和为17,把这个两位数的十位数字与个位数字对调,所得的数减去原数差为9,则这个两位数是89.分析 设原数的十位数字为a、个位数字为b,则原数为10a+b,对调位置后所得数为10b+a,根据题意列方程求解可得.
解答 解:设原数的十位数字为a,个位数字为b,
根据题意,得:$\left\{\begin{array}{l}{a+b=17}\\{10b+a-(10a+b)=9}\end{array}\right.$,
整理,得:$\left\{\begin{array}{l}{a+b=17}\\{-a+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=8}\\{b=9}\end{array}\right.$,
则这个两位数为10a+b=89,
故答案为:89.
点评 本题主要考查二元一次方程组的实际应用能力,根据题意表示出原数和对调位置后的数是依据相等关系列方程组的关键.

练习册系列答案
相关题目
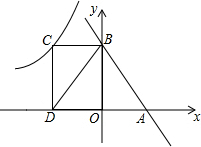 如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6.
如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6.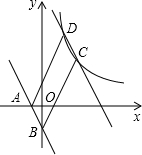 如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),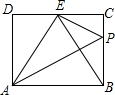 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )